JeroCaller

쌓여만 가는 빈 캔

3 분 소요

개요

프로그래밍 언어에서 사용할 수 있는 숫자 타입에는 정수(integer), 부동소수점(float), 복소수(complex)가 있다. 사람은 10진법에 익숙하나, 컴퓨터는 전기 신호 (전기가 들어오면 참, 안 들어오면 거짓)로 소통하기 위해 2진법을 사용한다. 그래서 컴퓨터는 정보를 비트(bit)로 표현한다. 또한, 2의 배수인 8진법, 16진법도 사용한다.

정수

파이썬에서 정수는 int로 나타내며, 불변형(immutable)이다. 불변형 객체에서는 변수와 객체 참조 간에 차이가 없다.

파이썬에서의 정수 크기는 적어도 32비트(4바이트)인데, 컴퓨터의 메모리에 의해 제한된다. 이는 C 또는 자바 내장 컴파일러에 따라 다르다. 정수를 나타내는데 필요한 바이트 수를 확인하려면 파이썬 3.1 이상 버전에서 (정수).bit_length() 메서드를 사용하면 된다.

print((100).bit_length())
print((1000).bit_length())

7
10

문자열로 표현된 정수 또는 다른 진법으로 표현된 숫자의 문자열 형태를 10진법 정수로 바꾸려면 int(문자열, 밑) 함수를 사용하면 된다.

number_string = '1100'
d = int(number_string)
print(d)

b = int(number_string, 2)
print(b)

1100
12

int() 함수의 두 번째 인자로 들어갈 수 있는 숫자는 2~36까지이다. 즉, 2진법에서 36진법까지의 수를 10진법으로 바꿀 수 있도록 해준다. 만약 밑에서 명시한 진법으로 표시할 수 없는 문자열을 대입한다면 ValueError 예외가 발생한다. 예를 들면, 아래 예제의 경우 12의 2는 2진법에는 없는 표현이므로 해당 예외가 발생한다.

print(int('12', 2))

ValueError: invalid literal for int() with base 2: '12'

부동소수점

컴퓨터에서 부동소수점을 표현하는 여러 방법 중 하나는 전기 전자 기술자 협회(IEEE)에서 개발한 IEEE 754로, 가장 보편적으로 쓰이는 표준이라고 한다.

파이썬에서 부동소수점은 float로 나타내며 불변형이다. 단정도(single precision) 방식에서 32비트 부동소수점을 나타낼 때 1비트는 부호(sign) (0: 양수, 1: 음수), 23비트는 유효 숫자 자릿수(significant digits, 가수(mantissa)라고도 한다), 8비트는 지수(exponent)를 나타내는 데에 쓰인다.

예를 들어, 십진수인 -118.625를 32비트 단정도로 표현해보자.

  1. 십진수의 절대값을 이진수로 변환한다.

    정수 부분

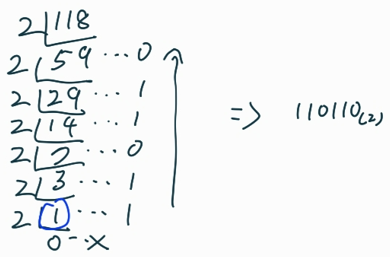
    정수 부분

    정수의 경우, 2로 나눈 나머지들이 이진수가 된다. 소수의 경우, 반대로 2로 곱한 값의 정수 부분이 이진수가 된다.

    3.PNG

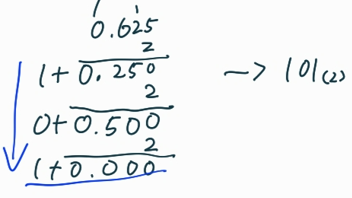
  • 소수점을 이진수로 바꿀 때 2를 나누는 게 아닌 곱하는 이유.

    4.PNG

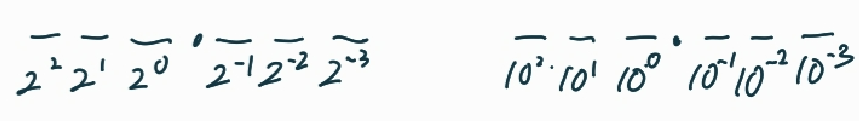
    소수부터는 음의 제곱이 붙기 때문. 이진법의 경우, 한자리씩 오른쪽으로 갈수록 2를 나눠줘야 한다. 따라서 10진법의 소수를 2진법으로 나눌 땐 역으로 2를 곱해줘야 한다. 정수부에선 왼쪽으로 갈수록 2를 곱해야 하는데, 10진법의 정수부를 2진법으로 나타내기 위해선 10진법의 정수부를 2로 나누는 것과 반대라고 생각하면 된다.

또한, 정수 부분을 이진수로 바꿀 때는 가장 마지막에 나온 나머지를 맨 왼쪽 자리에 기입했다. 앞서 정수 부분을 이진수로 변환할 때 가장 마지막에 나온 나머지는 1을 2로 나눈 나머지인 1이었다. 이 1이 이진수의 맨 왼쪽 자리를 차지하게 된다. 그러나 소수 부분을 이진수로 쓸 때는 순서가 정반대이다. 즉, 맨 처음에 곱하고 나온 정수 부분이 맨 왼쪽에 기입되는 것이다.

위에서 구한 정수부와 소수부를 합치면 다음의 이진값이 나온다.

\[118.625_{(10)} = 110110.101_{(2)}\]
  1. 부호를 표시한다.

앞서 구한 이진수에 부호를 나타내는 숫자도 맨 앞에 표시한다. 위 예의 경우 음수였으므로 1을 맨 앞에 붙인다. 그러면 1110110.101(2) 가 된다.

  1. 정규화하기.

이제 정규화한다. 여기서 정규화라는 것은 소수점 왼쪽에 단 한자리의 0이 아닌 숫자만 남기고 나머지는 지수로 표현하는 것이다. 예를 들면 12345를 1.23 * 10^4로 표현하는 것이다.

\[1110110.101_{(2)} = 1.110110101\ X \ 2^{6}\]

사실 위 과정에서 맨 앞에 부호를 나타내는 1비트를 첨가하였으므로 소수점 왼쪽 부분은 항상 부호를 나타내는 숫자가 된다.

1.11 … 으로 표시된 숫자를 (부호를 제외하고, 즉 소수점 오른쪽부터) 가수부(23비트)에 넣는다. 부족한 자릿수는 0으로 채운다.

\[11011010100000000000000\]

(총 23자리)

  1. 지수를 바이어스를 통해 표현하기

이제 지수 부분을 비트에 표현할 차례이다. 위 예에서는 6인데, 6을 이진수로 바꿔서 바로 넣지 않는다. 지수 부분에 바이어스를 더한다. 앞서 단정도 32비트 방식에서 지수 부분은 8비트로 표현한다고 하였다. 이 8비트로 나타낼 수 있는 가장 큰 수에서 1을 뺀 숫자인 \(2^8 -1 = 127\)을 지수 6과 더한 후, 이 결과값을 이진수로 바꾼다.

\[6_{(10)} + 127_{(10)} = 133_{(10)} = 10000101_{(2)}\]

따라서 -118.625를 32비트 단정도로 표현하면 다음과 같다.

  • 부호 비트: 1
  • 지수 비트: 1000010
  • 가수 비트: 111011010100000000000000

배정도(double precision) 방식에서는 64비트 부동소수점을 나타낼 때 1비트는 부호, 52비트는 가수, 11비트는 지수로 나타낸다. (배정도에서 바이어스는 1023 (\(2^{(10)} - 1)\)을 더한다)

위 과정에서 더 자세한 점들은 부동소수점에 관하여… 페이지 참고.

부동소수점끼리의 비교

대부분의 10진법 수들은 2진수로 정확하게 표현할 수 있으나, 2진수로 정확하게 표현하기 어려운 숫자도 존재한다. 예) 0.1(10) = 0.00110011001100…(2)

1.2 - 0.1 == 1.1
False
0.1 * 0.1 == 0.01
False
0.2 * 3 == 0.6
False

정확한 부동소수점을 사용하고자 한다면 decimal 모듈의 Decimal() 메서드를 사용하면 된다. 자세한 사항은 [decimal] 참조(해당 페이지 준비 중).

부동소수점 관련 함수

round(x, n) → n < 0일 경우, x를 정수 n번째 자리에서 반올림하여 그 값을 반환한다. n > 0일 경우 x를 소수점 이하 n번째 자리로 반올림한 값을 반환한다.

round(12.34, -1)
10.0
round(12.345, 2)
12.35

as_integer_ratio() 메서드는 부동소수점을 분수로 표현해준다.

0.75.as_integer_ratio()
(3, 4)

진법

bin(x) 메서드는 정수 x의 2진수를 문자열로 반환한다.

bin(100)
'0b1100100'

oct(x) 메서드는 정수 x를 8진수의 문자열로 반환한다.

oct(100)
'0o144'

hex(x) 메서드는 정수 x를 16진수의 문자열로 반환한다.

hex(100)
'0x64'

References

[1] 지은이: 미아 스타인, 옮긴이: 최길우, “파이썬 자료구조와 알고리즘”, (2019, 한빛미디어)

[2] [1]의 소스코드 https://git.io/fj0II

[3] Marina von Steinkirch, “An introduction to Python & Algorithms”, (2013)

[4] 소수점 이진수 변환과 2의 보수 변환

This content is licensed under CC BY-NC 4.0

댓글남기기

참고