[지식/이론][python] 부동소수점에 관하여

1의 보수

10진수 100은 2진수로 1100100이다. 8비트에 맞춰 8자리로 맞추면 01100100(2)이다. 같은 8자리 2진수인 11111111을 방금 이진수로 빼보자.

\[ \begin{split} 11111111\\ -01100100\\ ——–\\10011011\end{split} \]

위 결과값은 앞선 2진수 01100100의 각 비트를 0은 1로, 1은 0으로 바꾼 것과도 같다. 이와 같은 연산을 통해 얻은 2진수를 1의 보수라 한다. 위 예제에서는 10011011(2)가 1의 보수이다.

앞서 언급된 8자리에서 가질 수 있는 최대값인 11111111(2)는 10진수로 변환하면 255로 $2^8 -1$과 같은 수이다. 즉 1의 보수는…

\[1의\ 보수 = (2^E-1) - 원래\ 2진수\]

여기서 E는 원래 2진수의 최대 자리수이다. 앞선 예제는 8자리 수였으므로 E=8을 대입하여 진행되었다.

1의 보수로 계산 시 한 자리가 더 길어지는 경우에는 캐리 값을 결과값에 더한다.

   00100000  = 32
+  11111110  = -1 (1의 보수)
   ======
   100011110   = (맨앞 부호 제외) 30

   00011110
+  00000001
   ======
   00011111 = 31

위 예제에서 30의 이진수가 나올 때 앞선 덧셈 과정에서 맨 앞에 1이 더 붙었다. 이를 carry라 한다. 이 경우, 30에 carry값인 1을 더한다.

2의 보수

2의 보수는 2의 제곱수에서 어떤 이진수를 빼서 얻은 이진수를 말한다. 앞서 1의 보수와 정의가 비슷하다. 다만 1의 보수에서 존재했던 -1이 2의 보수에서 없을 뿐이다.

\[2의\ 보수 = 2^E - 원래\ 2진수\]

여기서 2^E는 2진수로 나타낼 때 주어진 2진수보다 자리수가 하나 더 높고, 가장 높은 자리가 1이며, 나머지는 0이어야 한다. 예) 주어진 2진수가 4자리일 경우 → 10000

또는 2의 보수는 어떤 이진수의 1의 보수를 구한 후, 그 결과값에 1을 더한 값과도 같다. 십진수 100은 2진수로 01100100인데 이 값의 2의 보수를 구하면 다음과 같다.

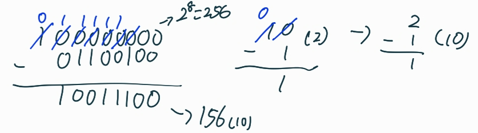
2의 보수를 바로 구하는 과정

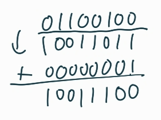
1의 보수를 구하고 거기에 1을 더해 2의 보수를 구하는 과정. 1의 보수를 구하려면 원래 2진수의 모든 자리수에 0은 1로, 1은 0으로 바꾸면 된다.

2의 보수에서는 보수를 구하는 과정에서 한 자리가 더 길어진 경우, 가장 높은 자리의 숫자를 버린다.

  01010000  => 80  
+ 11010000  => - 48 ( 48의 2의 보수)
  =======
 100100000
  =======
  00100000 => 32

위 예제를 보면, 덧셈 과정에서 한 자리가 더 추가되었다. 이 경우, 가장 높은 자리의 숫자인 1을 버린다. 그러면 00100000(2)가 남는데, 이 숫자는 10진법으로 32이다. 위 연산은 10진법으로 표현하면 80-48=32이다.

부동소수점에서 바이어스를 사용하는 이유

IEEE 754 표준을 이용하여 컴퓨터에서 부동소수점을 이용하는 과정에서, 실수를 정규화하고 나오는 지수 부분을 바로 비트로 표현하지 않고 바이어스를 먼저 더한 후에 그 결과값을 비트로 표현하였다. 이렇게 바이어스라는 개념을 추가하는 이유는 부호가 존재하는 2의 보수값은 값의 비교를 더 어렵게 하기 때문이다.

8비트 체계에서 보통 맨 앞의 비트는 부호를 표시하는 용도로 쓰인다. 이 상황에서 8비트 체계로 나타낼 수 있는 가장 큰 수는 01111111(2) = 127이다. 여기서 10(2)을 더하면 10000001(2) = -1이 되어버린다. 맨 앞 비트를 부호가 아닌 숫자를 표현하는데에 쓰였다면 +129가 되었을 것이다. 이렇게 부호 비트의 존재로 인해 혼동이 생겨버린다. 이렇게 수의 체계에 혼동이 발생하는 것을 방지하기 위해 바이어스를 추가한다.

n비트 체계에서 실수를 비트로 나타낼 때 실수를 정규화하고 나온 지수에 바이어스를 더한다. 여기서 바이어스는 $2^n-1$이다. 8비트 체계라면 2^8 - 1 = 127을 더한다. 만약 지수가 6이라면 여기에 127을 더한 133을 2진수로 표현한 값인 10000101(2)를 지수 비트에 넣는 것이다.

---

Reference

[1] 지은이: 미아 스타인, 옮긴이: 최길우, “파이썬 자료구조와 알고리즘”, (2019, 한빛미디어)

[2]

1의 보수

[3]

2의 보수

[4]

floating point는 왜 Bias(이하 Bias 표현법)를 사용할까? (목적, Bias 연산 등 예시)

[5]

Floating Point Numbers

This content is licensed under CC BY-NC 4.0