[자료구조] 우선순위 큐와 힙
우선순위 큐 (priority queue)
입력값이 단순히 값으로만 구성된 것이 아니라 (값, 우선순위)로 구성되어 있을 때, 가장 높은 우선순위를 가지는 데이터가 큐에서 먼저 반환되도록 고안된 자료구조를 우선순위 큐라고 한다. 여기서 우선순위는 그 숫자가 가장 큰 것이 우선순위가 높은 것이라고 가정하는 것(최대 이진 힙, max binary heap)과 가장 작은 것이 우선 순위가 높은 것이라고 가정(최소 이진 힙, min binary heap)하는 방법이 있다. 여기서는 우선순위를 표시하는 숫자가 가장 높은 데이터가 가장 높은 우선순위를 가진다고 가정하겠다.
우선순위 큐는 큐의 형태를 가지기는 하나, 우선순위가 높은 순대로 데이터를 추출하기에, 입력한 순서대로 추출된다는 보장이 없다.
우선순위 큐는 둘 이상의 데이터의 우선순위가 같을 때는 어떻게 해야 하는지 따로 정해진 규약은 없다.
우선순위 큐도 큐라서, 큐를 코드로 구현할 때 데이터를 큐에 넣는 enqueue()와 큐에서 데이터를 추출하는 dequeue() 기능을 포함한다. 그런데 앞서 말했듯, 우선순위 큐는 큐와는 달리 맨 처음 들어온 데이터가 빠져나가는 형태가 아닌 우선순위가 가장 큰 데이터가 먼저 빠져나가는 형태이기에 사용자가 dequeue() 메서드 호출 시 해당 데이터를 찾아서 반환시켜야 한다. 이 경우 큐가 배열이나 연결 리스트로 구현되어있다면 전체 데이터들 중 왼쪽에서부터 차례대로 우선순위가 가장 높은 데이터를 찾는 순차 탐색법을 사용할 수 있겠다. 그러나 최악의 경우 O(N)이라는 성능을 가진다. 하지만 힙(heap)이라는 자료 구조를 사용한다면 O(log N)의 시간복잡도를 가지는 우선순위 큐를 구현할 수 있어 더 효율적인 성능을 가질 수 있다.
최대 이진 힙 (max binary heap)
이진 힙은 다음과 같이 상위 계층에 있는 하나의 부모 데이터가 하위 계층에 있는 두 자식 데이터와 연결되어 있고 이 형태가 반복되는 구조를 띤다.
![그림 1. 최대 이진 힙 구조. (값, 우선순위)에서 우선순위만 표시되어 있다. [1] 참조.](/images/2023-06-15/2023-06-15-data-structure-priority-queue-heap-2.png)
그림 1. 최대 이진 힙 구조. (값, 우선순위)에서 우선순위만 표시되어 있다.
위 그림은 최대 이진 힙의 구조를 설명한 것이며, 우선순위 숫자가 가장 높은 데이터가 맨 위에 한 개로 존재하고, 아래로 내려갈수록 우선순위가 낮은 데이터가 존재하는 형태를 띤다. (최대 이진 힙은 우선순위를 나타내는 숫자가 가장 큰 데이터가 맨 위에 존재하도록 배치한다. 최소 이진 힙의 경우 반대로 숫자가 가장 낮은 데이터가 맨 위에 존재하게 된다) 위 그림을 자세히 보면, 부모 데이터와 직접 연결되어 있는 두 자식 데이터 간의 대소관계만 명확히 보이도록 정렬되어 있을 뿐 데이터 전체가 정렬되어 있진 않다. 그래서 위 그림의 2층에 있는 2는 3층에 있는 19보다 작음에도 2와 직접 연결되어 있는 부모 데이터의 우선순위(90)와의 대소관계만 고려되기 때문에 위와 같은 구조를 띨 수 있는 것이다.
이진 힙의 또 다른 특징은 k층에 있는 데이터의 수는 \(2^k\)만큼 존재한다는 것이다. 위 그림을 보면 0층에는 2^0 = 1개, 1층에는 2^1 = 2개, 2층에는 2^2 = 4개, 3층에는 2^3 = 8개가 있음을 알 수 있다.
정리하자면, 최대 이진 힙은 다음의 특성을 지닌다.
- 힙 순서 특성 (heap-ordered property) : 한 데이터의 우선순위는 왼쪽과 오른쪽의 자식 데이터의 우선순위보다 크거나 같아야 한다. 자식 데이터의 입장에서는 자식 데이터의 우선순위는 부모 데이터의 우선순위보다 작거나 같아야 한다.
- 힙 형태 특성 (heap-shape property) : k+1층에 데이터를 저장하기 전 k층에는 반드시 \(2^k\)개의 데이터들이 존재해야 한다. 이것만 지키면 맨 마지막 계층에는 데이터의 수가 \(2^k\)만큼 꽉 채워지지 않아도 된다. 또한 데이터를 힙에 채울 때는 맨 왼쪽부터 채운다.
필요한 계층의 수 계산
그렇다면 N개의 입력값들을 최대 이진 힙으로 구성시키기 위해서는 몇 개의 계층이 필요할까? 즉 k는 몇까지 존재해야 할까?
힙이 0층부터 시작한다고 가정하면, 입력값의 개수 N에 대해 0층부터 k층까지 총 k+1개의 층으로 구성된다.
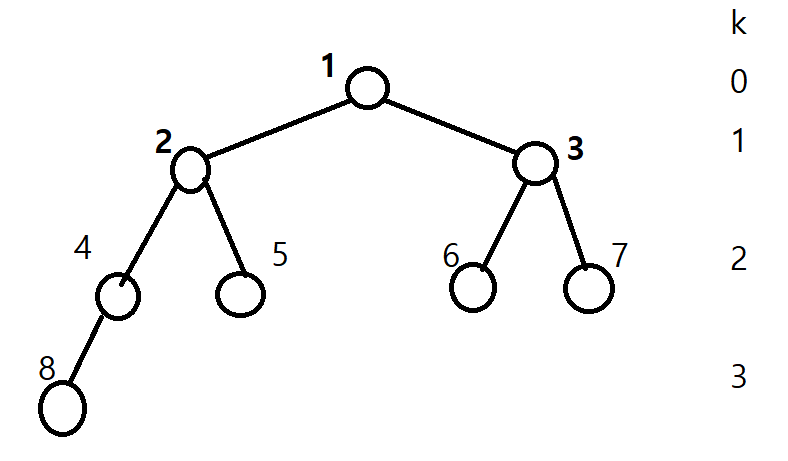
그림 2.
이 때, 입력값의 개수 N을 이진 힙으로 구성했을 때 빈 자리 없이 각 층을 꽉 채우는 경우(그림 2에서 맨 마지막 8번째 데이터를 제외했을 때)와 위 그림 2처럼 맨 마지막 층을 꽉 채우지 않는 경우로 나눠 생각해볼 수 있다.
- 각 층을 모두 채우는 경우
각 층을 모두 채울 때 입력값의 개수 N을 계산하고자 한다면 각 층의 데이터 개수 2^k를 모두 더하면 된다. 즉 이는 등비급수가 된다.
k=0, 1, 2, …일 때 각 층을 차지하는 데이터의 수를 등비수열로 나타내면 다음과 같이 나타낼 수 있다.
\[a_k = ar^k \ (k=0,\ 1, \ 2, ...)\]여기서 a는 첫번째 항(k=0일 때의 값), r은 공비이다. 이 등비수열을 0층부터 k층까지 모두 더한 값인 등비급수 \(S_k\)은 다음과 같이 구할 수 있다.
\[{\begin{align*}S_k &= a+ar+...+ar^k \\ rS_k &= \ \ \ \ \ \ \ ar+...+ar^k+ar^{k+1} \end{align*} \over (1-r)S_k = a-ar^{k+1}=a(1-r^{k+1})}\] \[\therefore S_k = \frac{a(r^{k+1}-1)}{r-1}\]이 문제에서 등비수열은 \(a_k = 2^k \ (k=0,\ 1,\ 2,…)\)이고, 따라서
\[N= S_k=2^{k+1}-1 \\ \therefore (k+1) = \log{(N+1)}\]N=7인 경우, log(7+1) = log 8 = 3으로, 0층부터 2층까지 총 3개의 층이 필요함을 알 수 있다.
- 맨 마지막 층에 빈자리가 남게 채우는 경우.
그림 2에서처럼 맨 마지막 층에 빈자리가 남게 채우는 경우도 있을 수 있다. 이 경우에 log(N+1)을 구하면 정수로 딱 떨어지지 않고 실수로 나올 것이다. 그러면 해당 값의 정수부만 취한 후, 거기에 1을 더하면 필요한 총 계층의 수가 나온다.
그림 2를 예로 들면 N=8이고, log(N+1) = log 9 ~ 3.17이다. 여기서 정수부인 3을 취하고 여기에 1을 더하면 이것이 k+1 = 4, 즉 총 필요한 계층의 수가 된다. 다시 말해, N=8일 경우 0층부터 3층까지 총 4개의 층이 필요하다는 뜻이다.
위의 증명과정이 이해하기 어려우면 다음의 결론만 기억하면 된다.
결론) 필요한 층 수는 log (N+1)을 계산했을 때 정수로 딱 나오면 해당 정수가 곧 필요한 층 수가 되고, 실수로 나오면 정수부에 1을 더한 값이 필요한 층 수가 된다.
기존의 이진 힙의 맨 마지막 층에 새로운 데이터들로 꽉 채우게 되면 맨 마지막 층에 존재하는 데이터의 수는 그 이전 층들의 총 데이터의 수보다 1만큼 더 크다. 예를 들어 N=7개의 데이터로 0층부터 시작하여 1 → 2 → 4 으로 구성했을 때 맨 마지막 층에 새로운 데이터들로 꽉 채우면 총 1 → 2 → 4 → 8으로 맨 마지막 층에는 7+1 = 8개의 새로운 데이터들로 꽉 채워지게 된다. 맨 마지막 층을 새로운 데이터들로 채웠을 때 총 데이터의 개수는 2N+1이 된다. (N=7 → 2N+1=15)
수학적 증명
기존 데이터들의 수를 \(S_k\) (모든 층을 꽉 채우는 경우)이라 하고, 다음 층을 새로운 데이터들로 꽉 채웠을 때 해당 층의 데이터 수를 \(a_{k+1}\)이라고 한다면,
\[N = S_k = 2^{k+1}-1 \\ a_{k+1}=2^{k+1}\] \[a_{k+1} - S_k = 2^{k+1}-(2^{k+1}-1)=1\]즉, 맨 마지막 층의 데이터 수는 그 이전 층들의 데이터들의 수의 총합보다 항상 1만큼 더 크다. 한 편,
\[\begin{align*}S_{k+1} &= 2^{k+2}-1 \\&= 2 \cdot2^{k+1}-1 \\ &=2 \cdot (N+1)-1 \\ &=2N+1 \end{align*}\]즉, 기존의 k층에서 1층을 더 채우면 총 데이터의 수는 2N+1이 된다.
힙에 새로운 데이터를 삽입하는 과정
앞서 설명한 최대 이진 힙에 새로운 데이터 하나를 삽입할 때 단순히 맨 끝 층의 빈 자리에 저장하기만 하고 끝내선 안된다. 새로 삽입된 데이터의 우선순위도 고려하여 힙 내부 구조를 재구성해야 하기 때문이다. 하지만 힙 내부 구조의 전체를 건드리지 않고 부분만 건드려서 재구성하는 방법이 있다.
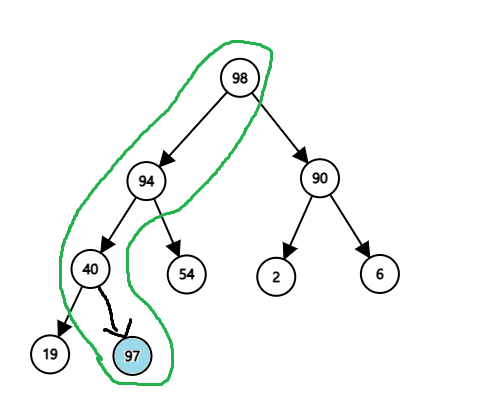
그림 3.
위 그림에서 기존의 최대 이진 힙의 맨 마지막 층의 왼쪽 부분에 우선순위가 97인 데이터를 삽입하였다. 공백없이 맨 마지막 층의 왼쪽부터 채웠기에 힙의 형태는 그대로 유지되나, 부모 데이터의 우선순위 40보다 자식 데이터의 우선순위 97이 더 크기에 힙 순위 특성을 위배하였다. 이를 해결하려면 다음의 과정을 거쳐야 한다.
- 새로 삽입한 데이터와 최상층인 0층의 데이터 사이에 최단 거리로 경로(path)를 긋는다. 위 그림 3에서는 초록색으로 0층까지 표시하였다. 그러면 경로 안에는 각자 다 다른 층수를 가진 데이터들만 모이게 된다.
- 경로의 맨 아래 층에 있는 데이터를 부모 데이터의 우선순위와 비교하고, 부모 데이터의 우선순위가 더 작으면 해당 부모 데이터와 위치를 바꾼다.
- 경로 내 0층부터 맨 아래층까지의 데이터들이 내림차순으로 정렬될 때까지 2번의 과정을 반복한다.
- 경로 내 0층부터 맨 아래층까지의 데이터들이 내림차순으로 정렬되어 힙 순서 특성을 만족시키면 위 과정을 멈춘다.
위 그림 3의 경로를 보면 0층부터 차례대로 98->94->40->97로 되어 있는데, 이를 위 2번부터 4번의 과정을 적용시키면 다음과 같이 정렬될 것이다.
- 98->94->97->40
- 98->97->94->40 (끝!)
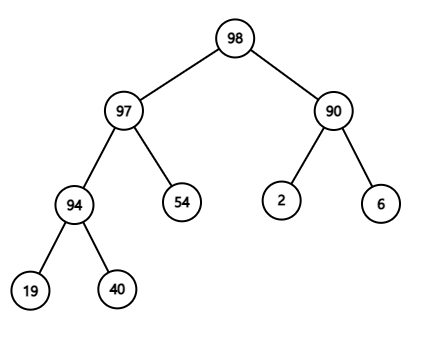
그림 4. 경로 내 데이터들의 우선순위를 최상층부터 내림차순으로 정렬을 완료한 모습.
정렬 과정에서 경로에 포함되지 않은 데이터들은 정렬에 영향을 받지 않아서 건드리지 않아도 힙 순서 특성을 자동으로 만족시킨다.
최악의 경우는 새로 저장된 데이터의 우선순위가 이미 기존에 존재하는 힙 내부의 경로 내 모든 데이터들의 우선순위보다 클 때이다. 그러면 해당 데이터는 0층까지 부모 데이터와 서로 자리를 바꾸는 연산을 해야 한다. 앞서 살펴보았듯, 힙을 구성하는 층수는 (k+1)이므로 최악의 경우 정렬 연산(부모 데이터와 자리를 뒤바꾸는 연산)은 k번 실행된다. 그리고 k = log (N+1) - 1이다. 즉, 최대 이진 힙에 새 데이터를 삽입하여 힙 내부가 재정렬될 때 최악의 경우 시간 복잡도는 O(log N)인 것이다. O(N)의 시간복잡도를 가지는 순차탐색법보다 더 효율적인 구조임을 알 수 있다.
최대 우선순위를 가지는 데이터 추출, 삭제하기
앞서 우선순위 큐에 대해 설명했을 때, 큐 내에서 데이터를 추출할 때에는 최우선순위를 가지는 데이터를 추출한다고 하였다. 우선순위 큐를 최대 이진 힙으로 구성했을 때, 0층에 있는 데이터를 그대로 추출하면 된다.
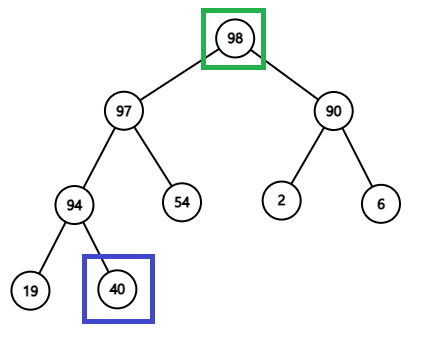
그림 5.
그런데 최상층인 0층에 있는 데이터를 추출하고 그대로 두면 안된다. 그러면 최상층이 된 1층에는 2개의 데이터가 존재하게 되어 힙 형태 특성을 위배한다. (앞서 그림을 통해 알 수 있듯, 항상 최상층의 데이터 수는 1개여야 한다) 이를 해결하려면 다음의 과정을 거치면 된다.
- 맨 아래층에서 맨 오른쪽에 있는 데이터를 힙 구조에서 떼어낸다. (그림 5에서 3층에 있는 우선순위 40의 데이터를 힙 구조와 분리시킨다) 이 때는 힙 형태와 순서 특성 모두 만족시킨다.
- 0층에 있는 데이터를 힙 구조에서 제거한 뒤 그 자리를 1번 과정에서 얻은 데이터로 바꾼다. (우선순위 40의 데이터가 0층에 자리잡는다) 이 때는 힙 형태는 유지되나 힙 순서 특성은 위배될 수 있다.
- 0층에 있는 데이터의 우선순위와 두 자식 데이터의 우선순위와 비교하여 0층에 있는 데이터의 우선순위가 더 작을 경우, 두 자식 데이터 중 우선순위가 더 큰 데이터와 자리를 바꾼다. (그림 5에서 0층의 자식 데이터가 존재하는 층인 1층을 보면 두 데이터의 우선순위 모두 0층의 부모 데이터의 우선순위 40보다 크다. 그러면 1층에 있는 두 자식 데이터 중 우선순위가 더 큰 97과 0층의 우선순위 40를 가지는 데이터와 자리를 바꾼다.) 만약 예를 들어 부모 데이터의 우선순위가 9이고, 왼쪽 자식 데이터의 우선순위는 8, 오른쪽 자식 데이터의 우선순위는 10일 때에는 오른쪽 자식 데이터와 위치를 바꾼다. 즉, 두 자식 데이터들 중 하나의 우선순위가 부모 우선순위보다 작아도 두 자식 데이터들 중 우선순위가 더 높은 데이터와 부모 데이터의 위치를 바꾸는 연산은 동일하게 적용된다.
- 3번의 과정으로 인해 한 층 아래로 내려간 데이터에 대해 그 데이터의 두 자식 데이터들의 우선순위와 비교하고, 두 자식 데이터의 우선순위가 더 높을 경우, 두 자식 데이터 중 우선순위가 더 높은 자식 데이터와 자리를 교체한다. 즉, 3번의 과정을 반복하는 것이다. 이를 힙 순서 특성을 만족할 때까지 반복한다.
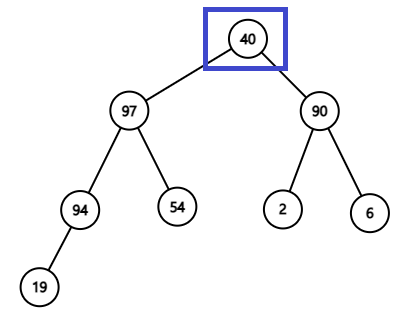
그림 6. 2번 과정을 묘사함.
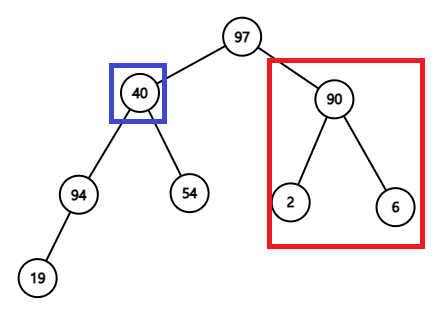
그림 7. 3번 과정을 묘사함. 참고로, 우선순위 40과 자리를 바꾼 97의 오른쪽 하위 트리 내 모든 노드들은 자동으로 우선순위 97보다 낮은 노드들만 존재하게 된다. 즉, 단순한 부모-자식 노드 간의 위치 교체는 다른 하위 트리의 우선순위에 영향을 끼치지 않아 힙 순서 특성을 위배하지 않는다.
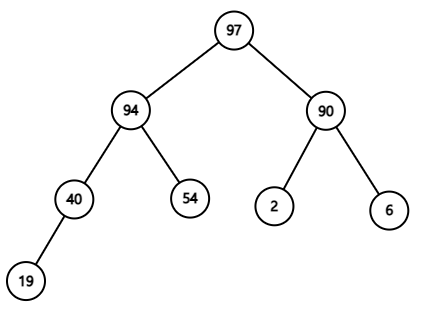
그림 8. 4번 과정을 묘사함. 정렬이 완료되었다.
앞서 데이터를 삽입할 때에는 맨 마지막 층에 삽입된 데이터가 윗층으로 올라가는 것에 비해 데이터를 삭제할 때에는 맨 마지막 층 맨 끝에 있던 데이터가 최상층으로 이동한 뒤, 우선순위 정렬에 따라 아래로 내려간다.
데이터 삭제 후 힙 내부 구조를 재구성하는 과정을 설명하였는데, 이 과정에서 최악의 경우 최상층으로 옮겨진 데이터가 최하층까지 k번 자리 바꿈하여 이동할 수 있다. 이 경우에도 시간복잡도는 O(log N)인 것이다.
즉, 이진 힙은 새로운 데이터를 삽입할 때도, 그리고 최우선순위의 데이터를 추출할 때에도 모두 최악의 경우 O(log N)의 시간복잡도를 가진다.
이진 힙을 배열에 담기
이진 힙을 하나의 배열에 담을려면 어떻게 담아야 할까?
배열은 인덱스가 0부터 시작하는데, 인덱스의 계산 편의를 위해 인덱스 1부터 이진 힙 내의 데이터를 채운다. 즉, 인덱스 0은 자리를 비운 채 놔둔다. 그리고 인덱스 1부터는 최상위층의 데이터부터 최하위층까지, 한 층에서는 맨 왼쪽부터 오른쪽까지 차례대로 배열에 담는다.
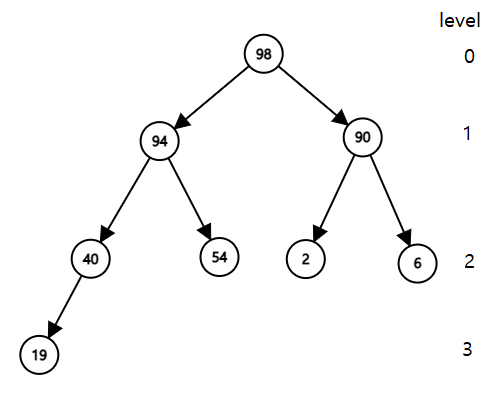
그림 9. 최대 이진 힙 예시.
index: [ 0 1 2 3 4 5 6 7 8]
array: [None, 98, 94, 90, 40, 54, 2, 6, 19]
예시 1. 그림 9의 최대 이진 힙을 배열로 나타냄.
그러면 배열의 왼쪽으로 갈수록 최상층에 가까워지고, 오른쪽으로 갈수록 최하위층에 가까워지는 것을 알 수 있는데, 그러면 특정 층에 존재하는 데이터의 자식 데이터를 참조하려면 어떻게 해야 할까?
위 그림 9와 예시 1을 보면 다음의 사실을 알 수 있다.
| 부모 데이터의 인덱스 위치 | 왼쪽 자식 데이터의 인덱스 위치 | 오른쪽 자식 데이터의 인덱스 위치 |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 4 | 5 |
| 3 | 6 | 7 |
| 4 | 8 | 9 (위 예시에선 존재하지 않음) |
즉, 배열 내 어떤 부모 데이터가 array[i]에 존재한다고 할 때, 해당 데이터의 왼쪽 자식 데이터는 array[2*i]에, 오른쪽 자식 데이터는 array[2*i+1]에 위치함을 알 수 있다. 단, 2i 또는 2i+1이 전체 입력값의 개수 N을 넘어서면 해당 데이터는 자식 데이터를 가지지 않는다. (그림 9에서, 인덱스 5에 위치한 데이터는 2*5 = 10 > N = 8이므로 자식 데이터를 가지지 않는다. 그리고 인덱스 4에 위치한 데이터는 2*4+1=9 > 8이므로 오른쪽 자식 데이터는 가지지 않는다)
반대로 자식 데이터의 기준에서 부모 데이터의 인덱스 위치는 어떻게 알까? 위 표를 보면 왼쪽 자식 데이터의 인덱스나 오른쪽 자식 데이터의 인덱스 모두 2로 나눈 몫이 바로 부모 데이터의 인덱스 위치임을 알 수 있다. 즉, 자식 데이터가 array[i]에 위치한다면 부모 데이터는 array[i // 2]에 위치한다는 뜻이다. 최상위층에 위치한 데이터는 부모 데이터가 없음에 유의한다. 즉, 부모 데이터를 찾기 위한 인덱스 연산은 i ≥ 2인 경우에만 적용시킬 수 있다는 것이다.
힙과 우선순위 큐를 파이썬 코드로 구현하기
"""
최대 이진 힙(Max Binary Heap)을 이용하여 우선순위 큐를 구현.
"""
from multipledispatch import dispatch
# type alias
Value = object
Priority = int
class Data():
def __init__(self, value: any = None, priority: int = 0) -> None:
"""
(값, 우선순위) 쌍의 데이터 객체. \n
매개변수 설명)\n
value: 데이터의 값. \n
priority: 데이터의 우선순위. 숫자가 높을 수록 최우선순위.
"""
self.value: any = value
self.priority: int = priority
class PriorityQueue():
"""
우선순위 큐의 최대 크기를 고정시키지 않고,
데이터가 들어오는 대로 저장하는 동적 방식 사용.
"""
def __init__(self, max_mode: bool = True) -> None:
"""
매개변수
------
max_mode: max binary heap으로 할 지에 대한 변수. \
True시 max binary heap, 즉 priority의 값이 큰 데이터가 힙 구조의 \
상위 계층에 위치하도록 함. False 시 min binary heap, 즉, priority 값 \
이 작은 데이터가 힙 구조의 상위 계층에 위치하도록 함. \n
인스턴스 속성
--------
self.heap_array: 인덱스 계산 편의상 배열 내 데이터의 저장 위치는 \
1부터 시작함. 즉, 인덱스 0은 비워둠. \n
"""
self.heap_array: list[Data] = [None]
self.N = len(self.heap_array) - 1
self.max_mode = max_mode
def __contains__(self, search: Value | Priority) -> bool:
"""
search가 우선순위 큐에 있는지 검사한 후, 존재하면 True,
그렇지 않으면 False 반환.
"""
# 매개변수 search의 자료형이 int가 아니라면 해당 변수는
# Value에 해당된다고 가정.
if type(search) != int:
for data in self.heap_array[1:]:
if search == data.value: return True
return False
else:
for data in self.heap_array[1:]:
if search == data.priority: return True
return False
def __repr__(self):
if not self.isEmpty():
return_data = []
for data_obj in self.heap_array[1:]:
return_data.append((data_obj.value, data_obj.priority))
return str(return_data)
else: return "None"
def clear(self) -> None:
"""
우선순위 큐 내부를 모두 비운다.
"""
del self.heap_array
self.heap_array: list[Data] = [None]
def showAll(self) -> list[tuple[Value, Priority]]:
"""
우선순위 큐 내 모든 데이터 반환.
"""
all_data = []
for data in self.heap_array[1:]:
all_data.append((data.value, data.priority))
return all_data
def isEmpty(self) -> bool:
"""
현재 우선순위 큐가 비어있는지 확인.
비어있으면 True 반환.
"""
return self.getCurrentSize() == 0
def getCurrentSize(self) -> int:
"""
현재 힙 내에 저장된 데이터의 수 업데이트 및 반환.
"""
self.N = len(self.heap_array) - 1
return self.N
def peek(self) -> Data | None:
"""
최우선순위 데이터를 반환.
검색만 하고 실제로 큐에서 제거하진 않는다.
"""
return self.heap_array[1] if not self.isEmpty() else None
def __isLess(self, a: Data | None, b: Data | None) -> bool | None:
"""
a < b ? \n
힙 내에 존재하는 두 데이터 간 우선순위의 대소를 비교 후,
a가 작으면 True, b가 작으면 False 반환.
만약 a, b 중 하나라도 None이면 None을 반환.
"""
if (a is None) or (b is None): return None
return a.priority < b.priority
def __switchData(self, a_index: int | None, b_index: int | None) -> None:
"""
힙 내에 두 데이터의 위치를 바꾼다.
바꾸고자 하는 두 데이터의 인덱스를 입력한다.
a, b 인덱스 매개변수 중 하나라도 None이면 아무런 작업을 수행하지 않음.
"""
if a_index is None or b_index is None: return
self.heap_array[a_index], self.heap_array[b_index] = \
self.heap_array[b_index], self.heap_array[a_index]
def __getParent(self, child_index: int) -> tuple[Data, int] | None:
"""
힙 내의 특정 데이터의 부모 데이터 및 부모 데이터의 인덱스를 반환.
부모 데이터가 존재하지 않으면 None을 반환.
"""
parent_index = child_index // 2
if parent_index >= 1:
return (self.heap_array[parent_index], parent_index)
return None
def __getChild(self, parent_index: int) \
-> tuple[tuple[Data, int] | tuple[None, None], tuple[Data, int] | tuple[None, None]]:
"""
힙 내의 특정 데이터의 두 자식 데이터를 반환.
자식 데이터가 존재하지 않으면 None을 반환.
"""
lchild_index = parent_index * 2
rchild_index = parent_index * 2 + 1
#if lchild_index <= self.N:
if lchild_index <= self.getCurrentSize():
lchild = (self.heap_array[lchild_index], lchild_index)
else: lchild = (None, None)
#if rchild_index <= self.N:
if rchild_index <= self.getCurrentSize():
rchild = (self.heap_array[rchild_index], rchild_index)
else: rchild = (None, None)
return (lchild, rchild)
@dispatch(object, int)
def enqueue(self, value: any, priority: int) -> None:
"""
새 데이터 입력.
매개변수
-------
value: 값.
priority: 우선순위 값.
"""
self.__enqueue(Data(value, priority))
@dispatch(tuple)
def enqueue(self, value_priority: tuple[any, int]) -> None:
"""
새 데이터 입력.
매개변수
-------
value_priority: (value, priority)
"""
self.__enqueue(Data(value_priority[0], value_priority[1]))
def __enqueue(self, new_data: Data) -> None:
"""
새 데이터 입력.
매개변수
---
new_data: Data(value, priority) 형태로 작성. \
반드시 Data 객체를 사용하여 값과 우선순위를 전달해야 함.
"""
self.heap_array.append(new_data)
# 힙 구조 재구성
target_index = self.getCurrentSize()
target_data = self.heap_array[target_index]
parent = self.__getParent(target_index)
while parent:
parent_data, parent_index = parent
if self.max_mode:
condition = self.__isLess(parent_data, target_data)
else:
condition = self.__isLess(target_data, parent_data)
if condition:
self.__switchData(parent_index, target_index)
target_index = parent_index
target_data = self.heap_array[target_index]
parent = self.__getParent(target_index)
else: break # 이미 경로 내 정렬이 모두 끝났으므로 작업 종료.
def dequeue(self) -> Data | None:
"""
최우선순위 데이터 반환 후 우선순위 큐 내에서 삭제.
큐 내에 데이터가 하나도 없으면 None 반환. \n
최대 이진 힙의 경우, 힙 구조 변경 시 두 자식 노드들 중 더 큰
우선순위 값을 가지는 자식 노드와 부모 노드의 위치를 바꾼다.
최소 이진 힙의 경우, 힙 구조 변경 시 두 자식 노드들 중 더 작은
우선순위 값을 가지는 자식 노드와 부모 노드의 위치를 바꾼다.
"""
try:
return_data = self.heap_array[1]
except IndexError:
print("우선순위 큐가 비어있어 추출할 데이터가 없습니다.")
return None
if self.getCurrentSize() <= 1:
# 힙 구조에 딱 하나의 값만 존재하는 경우 (그리고 해당 값을 삭제하려는 경우),
# 힙 구조를 재구성할 필요가 없다.
del self.heap_array[-1]
return return_data
# 힙 구조 재구성
self.__switchData(1, self.getCurrentSize())
del self.heap_array[-1]
target_index = 1
target_data = self.heap_array[target_index]
lchild, rchild = self.__getChild(target_index)
while (lchild or rchild) != (None, None):
lchild_data, lchild_index = lchild
rchild_data, rchild_index = rchild
if self.max_mode:
condition1 = self.__isLess(target_data, lchild_data) or \
self.__isLess(target_data, rchild_data)
else:
condition1 = self.__isLess(lchild_data, target_data) or \
self.__isLess(rchild_data, target_data)
condition2 = self.__isLess(lchild_data, rchild_data)
if condition1:
if condition2 is True:
if self.max_mode:
self.__switchData(target_index, rchild_index)
target_index = rchild_index
else:
self.__switchData(target_index, lchild_index)
target_index = lchild_index
target_data = self.heap_array[target_index]
elif condition2 is False:
if self.max_mode:
self.__switchData(target_index, lchild_index)
target_index = lchild_index
else:
self.__switchData(target_index, rchild_index)
target_index = rchild_index
target_data = self.heap_array[target_index]
else:
# if condition2 is None
if self.max_mode:
if rchild_data is None and self.__isLess(target_data, lchild_data):
self.__switchData(target_index, lchild_index)
else:
if rchild_data is None and self.__isLess(lchild_data, target_data):
self.__switchData(target_index, lchild_index)
target_index = lchild_index
target_data = self.heap_array[target_index]
lchild, rchild = self.__getChild(target_index)
else: break # 이미 경로 내 정렬이 모두 끝났으므로 작업 종료.
return return_data
def test_pq1():
test_dataset = [
('고양이', 15),
('개', 13),
('고슴도치', 14),
('호랑이', 9),
('사자', 11),
('바다사자', 12),
('족제비', 14),
('수달', 8),
('뱀', 2),
('소', 1),
('펭귄', 10),
('북극곰', 8),
('곰', 6),
('원숭이', 9),
('침팬치', 7),
('고릴라', 4),
('기린', 5),
('치타', 12),
]
#test_dataset = [('하마', -5), ('곰', -1)]
pq = PriorityQueue()
# enqueue 테스트
for data in test_dataset:
pq.enqueue(data)
print(pq)
print(f"Current size: {pq.getCurrentSize()}")
pq.enqueue('독수리', 9)
print(pq)
print(f"Current size: {pq.getCurrentSize()}")
# peek, dequeue 테스트
print(f"Result of search for pq: {pq.peek().value, pq.peek().priority}")
get_data = pq.dequeue()
print(f"data is {get_data.value}, priority is {get_data.priority}")
print(pq)
print(f"Current size: {pq.getCurrentSize()}")
def test_pq2():
test_data = [
('고양이', 13), ('개', 12), ('사자', 11), ('곰', 10), ('닭', 9)
]
pq = PriorityQueue()
for data in test_data: pq.enqueue(data)
print(pq)
pq.dequeue()
print(pq)
def test_min_pq():
test_data = [
('닭', 9), ('곰', 10), ('사자', 11), ('개', 12), ('고양이', 13)
]
pq = PriorityQueue(max_mode=False)
for data in test_data: pq.enqueue(data)
print(pq)
pq.dequeue()
print(pq)
def test_pq_negative_p():
test_data = [
('고양이', -12), ('사자', -13), ('치타', -11), ('곰', -4), ('바다사자', -7),
('개', -9), ('기린', -3),
]
pq = PriorityQueue(False)
for data in test_data: pq.enqueue(data)
print(pq)
pq.dequeue()
print(pq)
if __name__ == '__main__':
#test_pq1()
#test_pq2()
#test_min_pq()
test_pq_negative_p()
pass
import unittest
from priorityqueue import PriorityQueue
class TestPQ(unittest.TestCase):
def setUp(self) -> None:
self.test_data = [
('고양이', 15), ('개', 13), ('고슴도치', 14), ('호랑이', 9),
('사자', 11), ('바다사자', 12), ('족제비', 14), ('수달', 8),
('뱀', 2), ('소', 1), ('펭귄', 10), ('북극곰', 8),
('곰', 6), ('원숭이', 9), ('침팬치', 7), ('고릴라', 4),
('기린', 5), ('치타', 12),
]
def testEmptyPQ(self):
"""
우선순위 큐 생성 후 출력 테스트.
"""
pq = PriorityQueue()
self.assertEqual(pq.isEmpty(), True)
self.assertEqual(pq.getCurrentSize(), 0)
self.assertEqual(pq.__repr__(), "None")
self.assertEqual(pq.peek(), None)
self.assertEqual(pq.dequeue(), None)
self.assertEqual('곰' in pq, False)
def testEnqueue(self):
"""
데이터 삽입 테스트.
"""
pq = PriorityQueue()
# case 1
pq.enqueue('하마', 1)
self.assertEqual(pq.__repr__(), str([('하마', 1)]))
self.assertEqual(pq.getCurrentSize(), 1)
self.assertEqual(pq.isEmpty(), False)
# case 2
pq.enqueue(('곰', 12))
peek_data = pq.peek()
self.assertEqual(peek_data.value, "곰")
self.assertEqual(peek_data.priority, 12)
all_data = pq.showAll()
all_data.sort()
self.assertEqual(all_data, sorted([('하마', 1), ('곰', 12)]))
self.assertEqual(pq.isEmpty(), False)
self.assertEqual(pq.getCurrentSize(), 2)
self.assertEqual('곰' in pq, True)
self.assertEqual(1 in pq, True)
# case 3
pq.clear()
test_data = [
('독수리', 5), ('하마', 1), ('기린', 12)
]
for data in test_data:
pq.enqueue(data)
expected_result = [('기린', 12), ('독수리', 5), ('하마', 1)]
self.assertEqual(sorted(pq.showAll()), sorted(expected_result))
def testDequeue(self):
"""
데이터 추출 및 삭제 테스트.
"""
pq = PriorityQueue()
# case 1
pq.enqueue('곰', 12)
get_result = pq.dequeue()
self.assertEqual(get_result.value, '곰')
self.assertEqual(get_result.priority, 12)
self.assertEqual(pq.getCurrentSize(), 0)
self.assertEqual(pq.isEmpty(), True)
self.assertEqual(pq.showAll(), [])
# case 2
get_result = pq.dequeue()
self.assertEqual(get_result, None)
if __name__ == '__main__':
unittest.main()
우선순위 큐가 비어있어 추출할 데이터가 없습니다.
.우선순위 큐가 비어있어 추출할 데이터가 없습니다.
..
----------------------------------------------------------------------
Ran 3 tests in 0.001s
OK
Reference
[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)
This content is licensed under
CC BY-NC 4.0


댓글남기기