[자료구조] 해시 테이블 (hash table) (2)

해시 함수

해시 함수의 시간복잡도

해시 테이블에 쓰이는 해시 함수는 입력받은 키를 해싱하여 나온 해시 코드를 비킷의 인덱스로 사용하여 해당 버킷에 키와 쌍으로 연결된 value를 저장하는 구조를 띈다. 해시 함수는 해시 테이블에 저장하려는 입력값들의 크기 N에 상관없이 항상 일정한 연산 과정을 거쳐 해시 코드를 반환한다. 즉 해시 함수의 시간 복잡도는 O(1)이라고 할 수 있겠다.

hash(): 파이썬 내장 해시 함수

파이썬에서는 hash()라는 내장 해시 함수를 제공한다. 해당 함수의 입력값은 항상 불가변형 (immutable) 객체여야한다.

파이썬 3 버전부터는 코드를 실행시킬 때마다 hash() 의 반환값이 매번 달라진다. 즉, 예를 들어 같은 ‘a’라는 문자를 hash() 함수에 대입하더라도 그 반환값은 프로세스마다 달라지도록 설계되어있다. 이렇게 설계된 이유는 보안적인 이유 때문이라고 한다. 해커가 어떻게든 주어진 해시값과 충돌되는 똑같은 해시값을 내는 다른 키를 찾는 경우, 이를 해시테이블에 악용 시 해시테이블의 성능은 O(1)에서 O(N)으로 악화된다고 한다. 이를 이용해 서비스 거부 공격(denial-of-service attack, DOS)을 할 수 있다고 한다. 이를 방지하기 위해 hash() 함수는 프로세스마다 다른 값을 내도록 고안되었다고 한다.

다음은 문자열 ‘a’를 hash() 함수에 대입하여 그 해시 코드를 반환하여 출력하는 예제 코드이다.

key = 'a'
hash_code = hash(key)
print(hash_code)

-1855437115867578109

해시 코드가 매우 큰 숫자인데, 이를 해시 테이블에 적용할 수 있을 정도로 그 범위를 작게 만들려면 이 해시 코드를 해시 테이블의 전체 크기(즉, 총 버킷의 수) M으로 나눈 나머지를 이용하면 되겠다. (hash(key) % M) 그러면 이로부터 나올 수 있는 수들은 0부터 M-1까지이다.

해시 테이블

용어

• 체인(chain): 해시 코드가 같은 데이터들을 말한다. 분리 연결법(separate chaining)에서 한 버킷에 저장된 연결리스트 내 노드들이 하나의 체인이라고 볼 수 있다.

해시 테이블의 복잡도

입력값의 전체 크기 N에 대해, 입력값을 배열(array)에 입력하거나 검색하려면 최악의 경우 O(N)의 성능을 가진다. 이는 배열의 왼쪽부터 순차적으로 검색하기 때문이다. 그러나 해시 테이블의 경우, 주어진 키를 해싱하여 나온 값을 인덱스로 활용하여, 인덱스에 해당하는 버킷에 키와 연결된 value를 저장, 검색하는 구조이다. 따라서 해시 충돌이 없다고 가정하면 해시테이블에서의 값 저장 또는 검색의 시간복잡도는 O(1)이다. 즉, 데이터의 저장과 검색 측면에서 배열보다 해시테이블이 더 성능이 좋다.

해시 충돌의 경우

• 개방 주소법 (open addressing)

데이터 삽입 시 해시 충돌의 경우 빈 버킷을 찾기 위해 선형 탐색법(linear probing)을 사용하여 1칸씩 빈 버킷을 찾는 경우, 처음 인덱스에서 1칸씩 다음 칸으로 나아가 빈 버킷을 찾아간 후, 빈 버킷이 없으면 다시 처음 인덱스인 0으로 돌아가 빈 버킷을 찾는 구조이다.

빈 해시 테이블에 N개의 데이터를 입력하려고 한다. 최악의 경우, N개의 모든 키의 해시값이 다 똑같은 값으로 나왔다고 하자. 그러면 N-1개의 데이터들은 모두 선형 탐색법을 통해 빈 버킷을 찾아야 한다. 맨 첫 데이터는 해당 인덱스에 버킷이 비었으므로 그냥 데이터를 삽입하면 된다. 두 번째 데이터의 경우, 바로 이전 데이터가 해당 인덱스의 버킷에 존재하므로 그 다음 한 칸을 조사한 후 그 버킷에 저장된다. 세 번째 데이터는 이미 2개의 버킷이 연속으로 점유되어 있으므로, 2번의 빈 버킷을 조사한 후에 3번째 버킷에 저장된다. 즉, N개의 입력값들에 대해 빈 버킷을 조사하는 횟수는 다음과 같다.

\[1 + 2 + 3+ ... + (N-1) = \frac{N(N-1)}{2}\]

빈 버킷을 조사하는 평균 연산의 횟수는 여기서 전체 입력값의 크기 N으로 나눈 (N-1)/2가 된다. 즉, 개방 주소법의 선형 탐색법을 이용할 때 최악의 경우 빈 버킷을 조사하는 평균 횟수에 대한 (시간)복잡도는 O(N)이다.

개방 주소법을 사용하면 해시테이블에 데이터가 차면 찰수록 다음 데이터 입력 시 빈 버킷을 조사하는 횟수가 많아질 것이고, 따라서 데이터 삽입 성능이 점점 떨어질 것이다. 따라서 미리 해시테이블이 입력할 값들의 크기 N을 파악한 뒤, 해시 테이블의 크기를 이보다 더 큰 크기로 설정해야 해시 테이블의 효율성을 보장할 수 있다.

필요한 저장 용량 측면에서 보면, 효율성을 위해 입력값 N개를 해시 테이블에 저장하기 위해선 이보다 더 큰 M개의 버킷을 준비하도록 해야 한다. 따라서 개방 주소법의 경우 필요한 메모리 용량은 M에 비례한다고 볼 수 있다. → O(M)

• 분리 연결법 (separate chaining)

해시 테이블의 크기가 M이고, 입력값의 크기가 N일 때, 최악의 경우 하나의 버킷에 모든 입력값들이 연결리스트로 연결되어 저장될 것이다. 이 경우 총 데이터 공간은 M + N이라 할 수 있겠다. 앞서 개방주소법의 경우 효율성을 위해선 반드시 N < M이어야 했지만, 분리 연결법의 경우 해시 테이블의 크기 M에 상관없이 (심지어 N > M이더라도 한 버킷의 연결 리스트에 쭉 연결될 수 있다) 저장할 수 있다. 따라서 분리 연결법에서 필요한 메모리 용량의 복잡도는 O(M+N)이다.

시간복잡도의 경우, 이를 계산하기 위해서 연결 리스트의 각 노드에 접근하는 횟수를 핵심 연산으로 지정하겠다. 최악의 경우, 크기 M을 가지는 해시 테이블에 오로지 하나의 버킷에 모든 입력값 N개들이 연결 리스트로 연결될 것이다. 여기서 해당 연결 리스트에 새 데이터가 입력되려면 N개의 노드들을 검색한 후 그 다음 빈 노드에 데이터가 입력될 것이다. 따라서 분리 연결법에서의 시간복잡도는 O(N)이다. 시간 복잡도에 대해서, 개방주소법과 분리연결법 모두 O(N)으로 동일함을 알 수 있다.

해시테이블의 성능: 부하율 (load factor)

앞서 살펴보았듯, 개방 주소법과 분리 연결법 모두 시간복잡도는 O(N)이었다. 그러나 두 방법 모두 입력값의 크기 N과 비교하여 해시 테이블의 전체 크기 M이 상대적으로 작으면 작을 수록 해시 충돌의 확률이 높아지는데, 이 경우 개방 주소법의 데이터 입력의 시간적 성능이 분리 연결법에 비해 더 안좋아진다고 한다.

해시 테이블의 성능은 현재 해시 테이블에 얼마나 많은 데이터들이 저장되어있느냐에 달려있다. 즉, 데이터가 많이 저장되어 있을수록 해시 테이블의 성능은 더 안좋아진다.

컴퓨터 과학에서는 N / M을 해시 테이블의 부하율 (load factor)이라 하며, 보통 \(\alpha\) (alpha)로 표기한다.

분리연결법의 경우, 부하율은 각 연결 리스트의 평균 길이를 의미하며, 1이상의 값을 가질 수 있다. 반면, 개방 주소법의 경우 부하율은 점유된 버킷의 퍼센티지로 정의되며, 최고 부하율은 (M-1)/M으로 1보다 작다.

부하율이 0.75 이상을 넘길 경우 해시 테이블의 성능이 떨어지기 시작한다고 알려져 있다. 즉, 전체 해시 테이블의 4분의 3이 데이터로 꽉차기 시작하면 성능이 떨어지는 것이다. 이를 해결하려면 해시 테이블의 크기 M을 더 크게 늘려서 부하율을 0.75 이하로 떨어트려야 한다.

해시 테이블 크기 증가시키기

해시 테이블의 성능의 효율성을 유지시키기 위해선, 데이터가 많이 저장되어 부하율이 0.75 이상 넘길 경우 해시 테이블의 크기를 증가시켜 부하율을 낮춰야 한다. 대부분의 프로그래밍 언어에서는 이를 실행하기 위해 일련의 버킷들을 구현하는 새 배열을 준비한 후, 기본 배열 내에 저장된 데이터들을 복사하여 새 배열에 붙여넣는 방식을 취한다.

해시 테이블에 저장된 데이터를 크기가 증가된 새 해시 테이블로 복사하는 과정에서 시간 복잡도는 O(M)으로, 즉 해시 테이블의 크기에 비례한다(데이터의 복사를 핵심 연산으로 한다). 크기가 증가된 해시 테이블의 크기가 클수록, 그만큼 복사해야할 데이터의 수가 많다는 뜻이기 때문이다.

그런데 여기서 주의해야할 점이 있다. 어떤 해시 함수로부터 얻은 해시값을 해시 테이블의 전체 크기 M으로 나눈 값을 버킷의 인덱스로 취하는 방식을 채택한 경우, M이 바뀌기 때문에 기존 데이터들을 똑같은 위치에 복사해선 안된다. 만약 이렇게 하면 M이 바뀌었기 때문에 버킷의 인덱스가 달라져서 키를 입력하더라도 그에 해당하는 값을 못찾을 수도 있다.

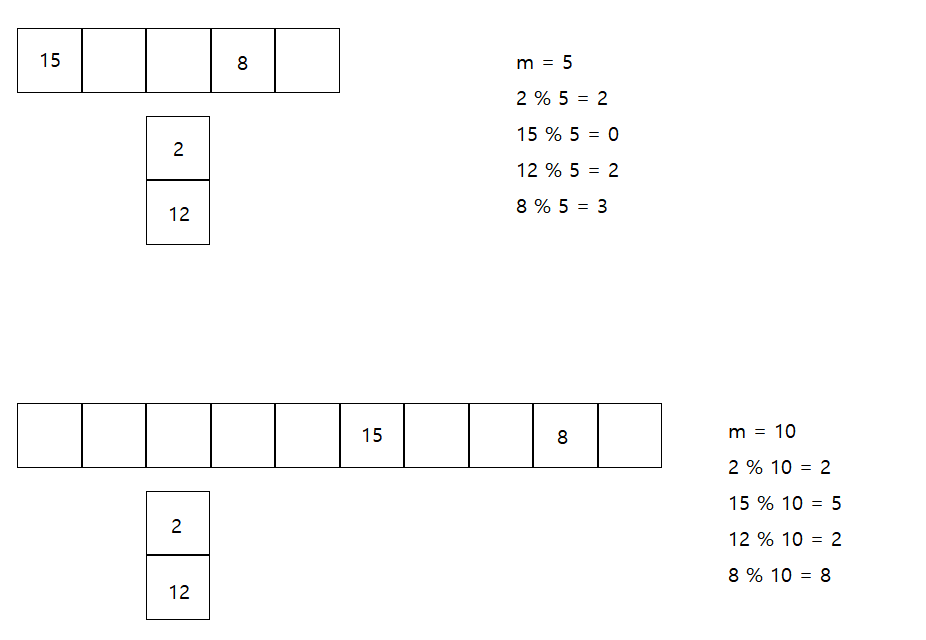
그림 1. M=5인 해시 테이블에 데이터 5개가 저장되어 있다. 이를 M=10인 해시 테이블로 데이터들을 옮겼을 때 결과물. 해시 충돌 해결책은 separate chaining을 이용하였다. 위 그림에서는 원래 각 버킷 당 연결리스트가 연결되어 있는 구조인데, 해시 충돌이 없는 버킷의 경우 편의상 버킷에 직접 그 키를 적었고, 해시 충돌이 일어난 버킷에만 연결 리스트를 그려넣었다.

위 그림 1처럼 해시 테이블의 크기는 증가하였으나 기존 데이터들을 똑같은 위치에 복사시킨 경우, 예를 들어 증가된 해시테이블에서 키가 15인 버킷을 찾으려고 하면 15 % 5 = 0이 되기에 인덱스가 0인 버킷을 조사한다. 그러나 위 그림 1를 보면 알 수 있듯 해당 인덱스에는 15가 존재하지 않고 텅 비어있다. 이렇게 엉뚱한 위치의 버킷을 참조하게 되는 셈이다.

따라서, 이를 해결하려면 복사 과정에서 모든 데이터들의 키값을 다시 해싱해야 한다. 즉, 각각의 키 값을 증가된 M에 따라 다시 해싱하여 얻은 인덱스 위치에 데이터를 복사해야 한다.

해시 테이블의 성능 효율성을 위해선 해시 테이블의 크기가 소수(prime number)이거나 홀수인 것이 좋다고 한다. 보통 new_M = 2M + 1로 잡아도 된다.

해시 테이블의 크기 M이 커지면 커질수록 크기 재조정(resizing)이 일어나는 빈도수는 낮아진다고 한다. 예를 들어 M의 크기를 두 배씩 한다고 하면, 2, 4, 6, 8, 16, 32, 64, 128, … 으로 증가할 것인데, 현재 M의 크기와 바로 이전의 M의 차이는 M의 크기가 클수록 그 차이가 커진다. 예를 들어 128 - 64 = 64는 64-32 = 32보다 더 크다. 즉, 이 차이만큼 크기 재조정하기 전까지 데이터를 많이 삽입할 수 있어 M이 클수록 크기 재조정하는 빈도수가 낮아진다.

중간에 동적으로 해시 테이블의 크기 조정 없이 N보다 충분히 큰 M으로 미리 해시 테이블의 크기를 정하고 해시 테이블에 데이터들을 입력하는 것과, 중간에 동적으로 해시 테이블의 크기를 조정하면서 데이터를 입력하는 과정을 반복하여 해시 테이블의 최종 크기가 M이 되도록 하는 방식과 비교할 때, 두 방법의 데이터 입력 시간은 3배 이상 차이나지 않는다고 알려져 있다. 여기에는 동적으로 해시 테이블 크기 증가 시 기존 데이터들의 키값을 다시 해싱하여 새 배열에 복사하여 붙여넣는 과정을 포함한 것이다.

---

Reference

[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)

This content is licensed under CC BY-NC 4.0