[알고리즘] 정렬 알고리즘
개요
숫자들을 정렬할 때에는 두 숫자의 위치를 얼마나 많이 바꿨는지(swap) 그 횟수도 중요하지만, 두 값의 대소비교를 한 횟수를 세는 것도 중요하다.
다음은 여러 정렬 방법들이 기술될 것인데, 모두 배열의 왼쪽부터 제일 작은 숫자가 들어가고, 배열의 오른쪽으로 갈 수록 더 큰 숫자가 정렬되는 오름차순 기준으로 설명될 것이다.
선택 정렬 (Selection sort)
선택 정렬은 배열 내에서 정렬되지 않은 숫자들 중 가장 작은 숫자를 찾아 이를 배열 왼쪽의 숫자와 자리를 바꿈으로써 정렬시키는 방법이다.
다음처럼 정렬되지 않은 8개의 숫자가 담긴 배열을 가정하자.
[12, 5, 4, 8, 3, 9, 1, 10]
맨 처음, 배열 내 가장 작은 숫자의 인덱스를 저장하는 변수인 min_idx를 생성한 후, min_idx = 0을 대입한다. 그리고 인덱스 1에 위치한 숫자부터 min_idx에 있는 숫자와 비교한다. 만약 인덱스 0에 위치한 숫자보다 더 작은 숫자를 발견하면 그 숫자의 인덱스를 min_idx에 저장하여 기록하고, min_idx에 위치한 숫자와 다음 남은 숫자들과 계속 비교하고 이를 반복한다. 배열의 끝까지 비교 연산을 통해 가장 작은 값의 인덱스를 찾았다면, 이를 인덱스 0에 위치한 숫자와 그 자리를 바꾼다.
[1, 5, 4, 8, 3, 9, 12, 10]
여기서는 1이 가장 작은 숫자이므로, 인덱스 0에 위치한 숫자 12와 그 자리를 바꾼다. 그 후, 인덱스 0을 제외한 나머지 숫자들 중 가장 작은 수를 찾아 이를 인덱스 1 위치의 숫자와 바꾼다. 이 과정을 반복하면 이 배열은 오름차순으로 정렬된다. 다음은 위 배열을 선택 정렬 방식으로 정렬하는 전체 과정을 묘사한다. 숫자 오른쪽에 V 표시는 해당 숫자는 이미 정렬되었다는 뜻이다.
[12, 5, 4, 8, 3, 9, 1, 10] 7번의 비교 연산을 거침
[1V, 5, 4, 8, 3, 9, 12, 10] 6번. 자리 교체 누적 1번.
[1V, 3V, 4, 8, 5, 9, 12, 10] 5번 자리 교체 2
[1V, 3V, 4V, 8, 5, 9, 12, 10] 4번 자리 교체 2
[1V, 3V, 4V, 5V, 8, 9, 12, 10] 3번 자리 교체 3
[1V, 3V, 4V, 5V, 8V, 9, 12, 10] 2번 자리 교체 3
[1V, 3V, 4V, 5V, 8V, 9V, 12, 10] 1번 자리 교체 3
[1V, 3V, 4V, 5V, 8V, 9V, 10V, 12V] 자리 교체 4
졍렬 결과
[1, 3, 4, 5, 8, 9, 10, 12]
두 숫자간 자리 교체 횟수에 상관없이, 두 숫자간 비교 연산은 7+6+5+4+3+2+1 = 28회를 거쳤음을 알 수 있다. 이를 일반화하면, N개의 크기를 가지는 배열에서 선택 정렬 시 필요한 비교 연산의 횟수는 \(\frac{N(N-1)}{2}\)이다. 즉, 최악의 경우 선택 정렬의 시간복잡도는 \(O(N^2)\)이다.
다음은 선택 정렬 알고리즘을 파이썬으로 구현한 코드이다.
from typing import Sequence
# type alias
Array = Sequence
Index = int
def selection_sort(array: Array) -> Array:
N = len(array)
for i in range(N-1):
min_idx = i
for j in range(i+1, N):
if array[j] < array[min_idx]:
min_idx = j
array[i], array[min_idx] = array[min_idx], array[i]
return array
삽입 정렬 (Insertion sort)
삽입 정렬은 배열의 맨 왼쪽 한 칸부터 시작하여 해당 칸이 이미 정렬된 부분 배열이라고 가정한다. 그 후, 왼쪽에서 두 번째에 존재하는 숫자를 정렬된 부분 배열로 포함시킨다. 이 때, 이미 정렬된 부분 배열에 존재하는 첫 번째 값과 대소비교를 한 후, 새로 들어온 두 번째 값이 더 작으면 서로 위치를 바꾼다. 그 후 세 번째 숫자를 정렬 배열에 포함시키고 이러한 과정을 반복한다.
다음은 삽입 정렬의 과정을 묘사한 예제이다. 괄호 () 로 둘러싸인 부분은 정렬된 부분 배열의 범위를 의미한다.
[12, 5, 4, 8, 3, 9, 1, 10]
[(12), 5, 4, 8, 3, 9, 1, 10]
[(12, 5), 4, 8, 3, 9, 1, 10]
[(5, 12), 4, 8, 3, 9, 1, 10]
[(5, 12, 4), 8, 3, 9, 1, 10]
[(5, 4, 12), 8, 3, 9, 1, 10]
[(4, 5, 12), 8, 3, 9, 1, 10]
[(4, 5, 12, 8), 3, 9, 1, 10]
[(4, 5, 8, 12), 3, 9, 1, 10]
[(4, 5, 8, 12, 3), 9, 1, 10]
[(4, 5, 8, 3, 12), 9, 1, 10]
[(4, 5, 3, 8, 12), 9, 1, 10]
[(4, 3, 5, 8, 12), 9, 1, 10]
[(3, 4, 5, 8, 12), 9, 1, 10]
[(3, 4, 5, 8, 12, 9), 1, 10]
[(3, 4, 5, 8, 9, 12), 1, 10]
[(3, 4, 5, 8, 9, 12, 1), 10]
[(3, 4, 5, 8, 9, 1, 12), 10]
[(3, 4, 5, 8, 1, 9, 12), 10]
[(3, 4, 5, 1, 8, 9, 12), 10]
[(3, 4, 1, 5, 8, 9, 12), 10]
[(3, 1, 4, 5, 8, 9, 12), 10]
[(1, 3, 4, 5, 8, 9, 12), 10]
[(1, 3, 4, 5, 8, 9, 12, 10)]
[(1, 3, 4, 5, 8, 9, 10, 12)]
선택 정렬의 경우, 처음부터 비교 연산을 통해 가장 작은 숫자를 찾은 후에 이를 배열의 왼쪽에 위치시킨 것에 비해, 삽입 정렬은 우선 정렬된 배열 내에 숫자를 삽입한 다음에, 정렬된 배열 내에서 대소 비교를 통해 정렬시킨다. 즉, 선택 정렬은 선비교, 삽입 정렬은 후비교를 하는 것이다.
최악의 경우, 필요한 비교 연산의 수는 1+2+3+4+5+6+7 = 28이다. 일반화하면 \(\frac{N(N-1)}{2}\)로, 선택 정렬과 같다. 따라서 삽입 정렬의 최악의 경우 시간복잡도는 \(O(N^2)\)으로 선택 정렬의 것과 똑같다. \(O(N^2)\)의 시간복잡도를 가지는 알고리즘은 보통 비효율적이라고 한다. 그리고 선택 정렬보다는 삽입 정렬이 조금 더 효율적이라고 한다.
재귀 함수와 분할 정복 (Recursion and divide and conquer)
재귀 함수는 함수 정의 내부에서 자기 자신을 호출하는 구조를 띤다.
def factorial(n):
if n <= 1:
return 1
return n * factorial(n-1)
위 예제는 주어진 n이란 정수에 대해 n! (팩토리얼)을 구하는 함수이다. 해당 함수를 보면 내부에 자기 자신을 호출하는 코드가 있음을 알 수 있다.
재귀 함수를 구현하려면 다음의 사항들이 반드시 고려되어야 한다.
- base case: 재귀 함수가 무한히 재귀 호출하는 것을 방지하기 위한 코드. 위 예제의
if n ≤ 1: return 1이 해당. - recursive case: 재귀 함수가 자기 자신을 호출하는 경우.
return n * factorial(n-1)에 해당. - 함수 내에서 자기 자신을 호출할 때 입력값을 원래 입력값보다 크거나 작은 값을 입력하여 무한 재귀 호출을 방지해야 한다. 즉, 재귀 호출을 할 때마다 해당 함수에 대입되는 입력값을 달리해야 한다. 만약 위 팩토리얼 예제의 맨 마지막 코드에 factorial(n)이라고 명시했다면 아무리 base case가 존재하더라도 무한 재귀 호출될 수 있다.
재귀 함수를 이용하면 원래 문제를 아주 작은 부분들로 쪼개고, 각 부분에서 문제를 해결한 다음, 이 쪼개진 부분들을 다시 합치는 방식을 통해 문제를 해결하는 분할 정복(divide and conquer) 방법을 사용할 수 있다.
다음은 재귀 함수를 이용하여 분할 정복 방식을 통해 주어진 숫자 배열 내에서 최대값을 찾는 알고리즘을 구현한 코드이다.
def find_max(array):
N = len(array)
if N == 1: return array[0] # base case
left_idx = 0
right_idx = N-1
mid_idx = (left_idx + right_idx) // 2
left_max = find_max(array[left_idx:mid_idx+1]) # recursion case
right_max = find_max(array[mid_idx+1:right_idx+1]) # recursion case
return max(left_max, right_max)
if __name__ == '__main__':
test_data = [12, 5, 4, 8, 3, 9, 1, 10]
result = find_max(test_data)
print(result) # 출력결과: 12
위 알고리즘은 주어진 배열의 중간지점을 기준으로 왼쪽과 오른쪽 부분 배열로 쪼개고, 쪼개진 부분 배열에 대해서도 두 개로 계속 쪼갠다. 이를 각 부분 배열의 크기가 1이 될 때까지 쪼갠다. 그 후, 쪼개진 왼쪽 부분 배열 중 가장 큰 숫자와 오른쪽 부분 배열 중 가장 큰 숫자 둘을 비교하여 이 중 더 큰 숫자를 반환하고, 이러한 과정을 단 하나의 최대값이 나올 때까지 반복한다. 그러면 원래 배열에서의 최대값을 반환하게 된다. 이렇게 최대값을 찾기 위해 배열을 아주 작은 크기로 나눈 후에 비교 연산을 처리한 후, 각각의 결과들을 다시 “조립”하여 최종 결과를 내는 분할 정복 방식이 사용된 것이다.
다음은 위 알고리즘 실행 과정을 묘사한 예제이다.
[12, 5, 4, 8, 3, 9, 1, 10] -> 원래 배열
[12, 5, 4, 8], [3, 9, 1, 10]
[12, 5], [4, 8], [3, 9], [1, 10]
각 부분 배열에서 최대값 반환
(12, 8), (9, 10)
(12, 10)
(12) -> 원래 배열 내에서의 최대값
합병 정렬 (merge sort)
합병 정렬은 앞서 설명한 재귀 분할 정복 방식을 이용하여 배열을 정렬하는 방법이다.
[12, 5, 4, 8, 3, 9, 1, 10]
[12, 5, 4, 8], [3, 9, 1, 10]
([12, 5], [4, 8]), ([3, 9], [1, 10])
([12], [5]), ([4], [8]), ([3], [9]), ([1], [10])
각 부분 배열 내에서 정렬
([5, 12], [4, 8]), ([3, 9], [1, 10])
[4, 5, 8, 12], [1, 3, 9, 10]
[1, 3, 4, 5, 8, 9, 10, 12]
먼저 주어진 배열을 반으로 계속 쪼갠다. 이는 부분 배열의 크기가 1이 될 때까지 쪼갠다. 이러면 두 개의 부분 배열 내에 있는 숫자들끼리의 비교 연산을 수월하게 할 수 있다. 두 부분 배열 간에 비교 연산을 하여 오름차순에 맞게 자리 바꿈하여 정렬한 후, 이들을 하나로 계속 합쳐나간다. 이 과정을 반복하여 쪼개진 부분 배열들이 다시 원래 배열의 크기가 될 때까지 합치면 최종적으로 오름차순으로 정렬된 배열을 얻게 된다.
- 쪼개지고 정렬된 부분 배열들을 합치는 방법
예를 들어 다음처럼 쪼개진 두 개의 부분 배열들이 존재한다고 가정하자. 이 때, 각 부분 배열들은 이미 정렬된 상태이다.
부분 배열 1: [4, 5, 8, 12]
부분 배열 2: [1, 3, 9, 10]
정렬된 배열: []
1단계)
부분 배열 1의 가장 작은 숫자: 4
부분 배열 2의 가장 작은 숫자: 1
두 수 중 가장 작은 수: 1
정렬된 배열: [1]
현재 부분 배열 현황)
부분 배열 1 : [4, 5, 8, 12]
부분 배열 2 : [3, 9, 10]
2단계)
부분 배열 1의 가장 작은 숫자: 4
부분 배열 2의 가장 작은 숫자: 3
두 수 중 가장 작은 수: 3
정렬된 배열: [1, 3]
부분 배열 1: [4, 5, 8, 12]
부분 배열 2: [9, 10]
3단계)
부분 배열 1의 가장 작은 숫자: 4
부분 배열 2의 가장 작은 숫자: 9
두 수 중 가장 작은 수: 4
정렬된 배열: [1, 3, 4]
부분 배열 1: [5, 8, 12]
부분 배열 2: [9, 10]
4단계)
부분 배열 1의 가장 작은 숫자: 5
부분 배열 2의 가장 작은 숫자: 9
두 수 중 가장 작은 수: 5
정렬된 배열: [1, 3, 4, 5]
부분 배열 1: [8, 12]
부분 배열 2: [9, 10]
5단계)
부분 배열 1의 가장 작은 숫자: 8
부분 배열 2의 가장 작은 숫자: 9
두 수 중 가장 작은 수: 8
정렬된 배열: [1, 3, 4, 5, 8]
부분 배열 1: [12]
부분 배열 2: [9, 10]
6단계)
부분 배열 1의 가장 작은 숫자: 12
부분 배열 2의 가장 작은 숫자: 9
두 수 중 가장 작은 수: 9
정렬된 배열: [1, 3, 4, 5, 8, 9]
부분 배열 1: [12]
부분 배열 2: [10]
7단계)
부분 배열 1의 가장 작은 수: 12
부분 배열 2의 가장 작은 수: 10
두 수 중 가장 작은 수: 10
정렬된 배열: [1, 3, 4, 5, 8, 9, 10]
부분 배열 1: [12]
부분 배열 2: []
8단계)
(마지막으로 남은 수를 정렬된 배열에 추가)
정렬된 배열: [1, 3, 4, 5, 8, 9, 10, 12]
각 부분 배열들을 가장 작은 수가 입구 끝에 있는 스택이라고 생각하면 되겠다. 각 부분 배열에서 가장 작은 수를 서로 비교한 후, 둘 중 가장 작은 수를 꺼내 새로운 배열에 추가한다. 그 후 또 각 배열에서 가장 작은 수끼리 비교하여 그 중에서도 가장 작은 수를 뽑아 새로운 배열에 추가하는 과정을 반복한다. 이러한 과정은 두 부분 배열 중 하나가 모두 소진될 때까지 반복되며, 남은 부분 배열 하나는 그대로 정렬된 배열 뒤에 덧붙이면 된다.
합병 과정에서 비교 연산의 횟수는 부분 배열 크기의 2배를 한 값과 동일하다. 위 예제에서는 크기가 4인 부분 배열 2개를 하나로 합치므로 총 8번의 비교 연산을 수행한다.
한 편, 두 부분 배열을 합치는 과정에서 새로운 배열이 필요함을 알 수 있다. 즉, 합병 정렬은 별도의 추가적인 메모리가 필요하다는 뜻이다.
합병 정렬의 시간복잡도
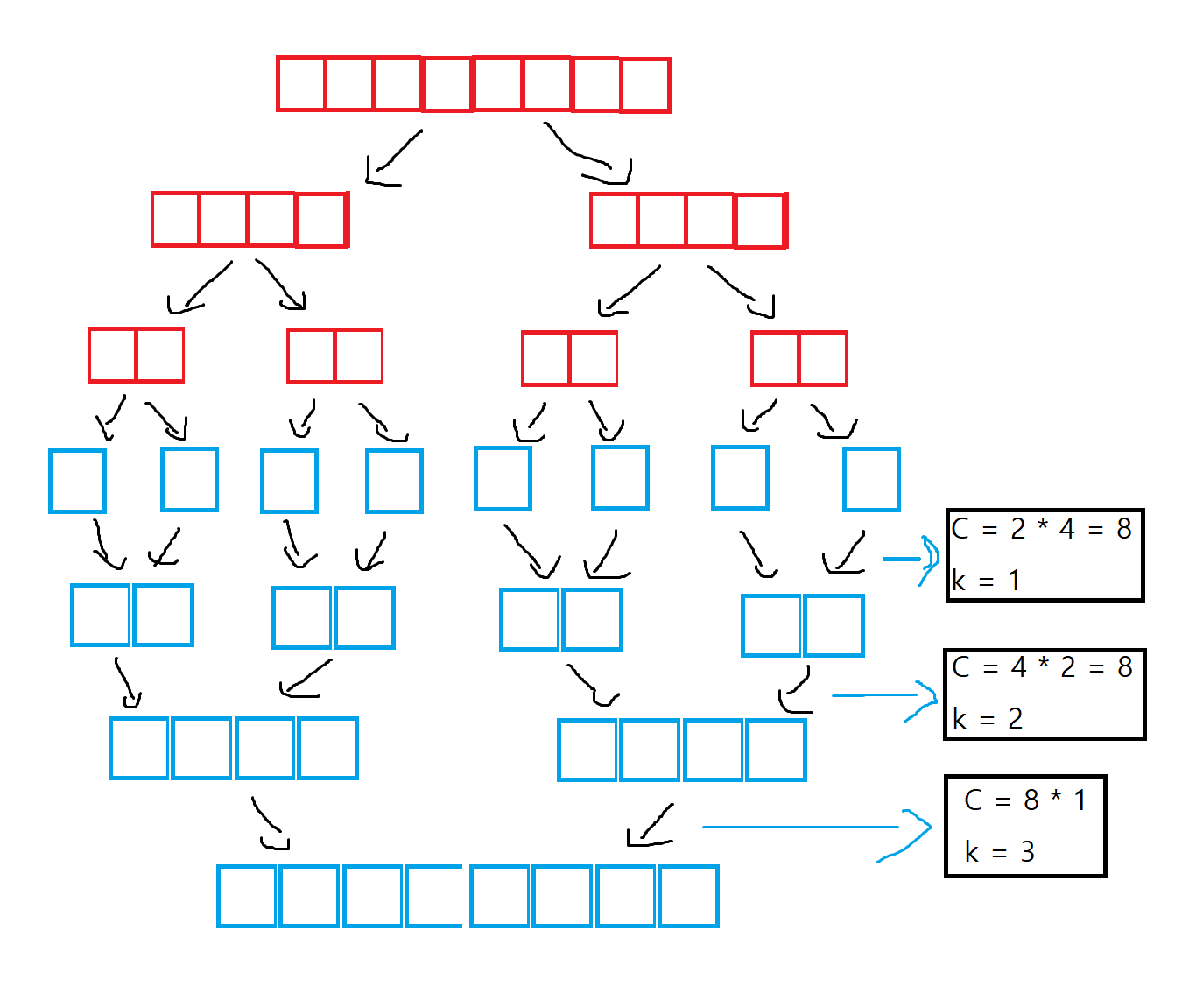
그림 1
분할하는 데에는 따로 비교 연산이 수행되지 않기에 분할에 대한 시간복잡도는 고려하지 않아도 된다.
쪼개진 부분 배열들을 하나로 합치는데 필요한 총 합병 단계(층 수)는 \(k = log(N)\)이다. 위 그림 1을 보면 N=8일 때 필요한 총 합병 단계의 수는 log 8 = 3임을 알 수 있다. 이 합병 단계의 수는 재귀 함수에서 함수를 재귀적으로 호출하는 깊이로도 볼 수 있겠다.
또한 각 단계마다 총 N개의 비교 연산을 한다. 따라서 합병 정렬의 최악의 경우 시간복잡도는 이 둘을 곱한 O(N log N)이다.
구현 코드
def merge_sort(array: Array) -> Array:
N = len(array)
def recursive_sort(low_idx: int, high_idx: int) -> None:
if low_idx >= high_idx: return
mid_idx = (low_idx + high_idx) // 2
recursive_sort(low_idx, mid_idx)
recursive_sort(mid_idx + 1, high_idx)
merge(low_idx, mid_idx, high_idx)
def merge(low_idx: int, mid_idx: int, high_idx: int) -> None:
l_sub_array = array[low_idx:mid_idx+1]
r_sub_array = array[mid_idx+1:high_idx+1]
lp = low_idx
rp = mid_idx + 1
for i in range(low_idx, high_idx+1):
if l_sub_array == []:
# 왼쪽 부분 배열이 합병 배열에 모두 들어간 경우.
# 남은 오른쪽 부분 배열을 합병 배열에 모두 넣는다.
array[i] = r_sub_array[0]
del r_sub_array[0]
elif r_sub_array == []:
# 오른쪽 부분 배열이 합병 배열에 모두 들어간 경우.
# 남은 왼쪽 부분 배열을 합병 배열에 모두 넣는다.
array[i] = l_sub_array[0]
del l_sub_array[0]
elif l_sub_array >= r_sub_array:
array[i] = r_sub_array[0]
del r_sub_array[0]
else:
array[i] = l_sub_array[0]
del l_sub_array[0]
recursive_sort(0, N-1)
return array
퀵 정렬 (Quick sort)
분할-정복 전략을 사용하는 또 다른 정렬 알고리즘으로 퀵 정렬이 존재한다. 퀵 정렬은 배열 내에서 pivot (기준값이라 보면 된다) 값을 선택한 후, 해당 값을 기준으로 왼쪽에는 피벗 값보다 작은 값들을, 오른쪽에는 피벗 값보다 큰 값들만을 나눠 분류시킨다. 이를 분할(partition)이라 하는데, 두 개로 분할된(divided) 부분 배열들에 대해서도 계속 재귀적으로 분할(partition)시킨다. (피벗값이 아주 작은 값이라 배열의 맨 왼쪽으로 위치하는 경우 2개의 부분 배열로 분할되지 않는 경우도 있긴 하다) 처음에는 피벗값을 기준으로 숫자들을 분류해도 피벗값의 양쪽에 있는 숫자들은 오름차순으로 정렬된 상태가 아닐 수도 있다. 하지만 분할-정복을 통해 계속 부분 배열로 쪼개서 분할 작업을 실행하면 결국 전체 배열은 오름차순으로 정렬된다.
합병 정렬할 때 항상 왼쪽 부분 배열의 크기와 오른쪽 부분 배열의 크기가 동일했던 것과 달리, 퀵 정렬에서는 피벗값을 기준으로 나눠진 왼쪽 부분 배열과 오른쪽 부분 배열의 크기가 똑같지 않을 수도 있다.
피벗값을 정하는 기준은 항상 배열의 첫 번째 또는 마지막에 있는 값을 피벗값으로 정할 수도 있고, 그냥 임의의 위치에 존재하는 값을 피벗값으로 선택할 수 있다.
다음은 주어진 배열을 퀵 정렬 알고리즘으로 정렬하는 과정을 대략적으로 묘사한 예제이다. 피벗값은 항상 배열의 첫 번째 값으로 하는 것을 가정하였다. 피벗값은 소괄호 ()로 표시하였다.
[12, 5, 4, 8, 3, 9, 1, 10]
[(12), 5, 4, 8, 3, 9, 1, 10]
[5, 4, 8, 3, 9, 1, 10, (12)]
[(5), 4, 8, 3, 9, 1, 10, (12)]
[4, 3, 1, (5), 8, 9, 10, (12)]
[(4), 3, 1, (5), (8), 9, 10, (12)]
[3, 1, (4), (5), (8), 9, 10, (12)]
[(3), 1, (4), (5), (8), (9), 10, (12)]
[1, (3), (4), (5), (8), (9), 10, (12)]
[(1), (3), (4), (5), (8), (9), (10), (12)]
정렬 결과)
[1, 3, 4, 5, 8, 9, 10, 12]
최선의 경우는 피벗값을 기준으로 분할된 왼쪽 부분 배열과 오른쪽 부분 배열의 크기가 동일한 경우이다. 이는 앞서 합병 정렬의 그림 1의 상황과도 똑같다. 이 경우의 시간복잡도는 O(N log N)이다. 최악의 경우, 부분 배열로 쪼갤 때마다 피벗값이 항상 해당 배열의 최소값만 걸려서 피벗값이 맨 왼쪽에 위치하는 경우이다. 이러한 양상은 선택 정렬과도 똑같기에 이 경우 시간복잡도는 \(O(N^2)\)이다. 이는 최악의 경우, O(N log N) 의 시간복잡도를 가지는 다른 알고리즘과 비교되는 부분이다. 이러한 이유로, 보통 피벗값을 정할 때는 매번 배열의 첫 번째 요소를 선택하지 않고, 배열 내 임의의 값을 피벗값으로 지정한다.
시간복잡도에서 약점이 있지만, 공간복잡도 측면에서 보면 병합 정렬에 비해 추가 메모리 용량을 필요로 하지 않는다는 장점도 존재한다.
다음은 퀵 정렬 알고리즘을 구현한 코드이다.
def quick_sort(array: Array) -> Array:
import random
def recursive_qsort(low_idx: Index, high_idx: Index) -> None:
if low_idx >= high_idx: return
init_pivot_idx = random.randint(low_idx, high_idx)
#init_pivot_idx = low_idx
final_pivot_idx = partition(low_idx, high_idx, init_pivot_idx)
recursive_qsort(low_idx, final_pivot_idx-1)
recursive_qsort(final_pivot_idx+1, high_idx)
def partition(low_idx: Index, high_idx: Index, p_idx: Index) -> Index:
"""
피벗값을 기준으로 피벗값보다 작은 값들은 피벗값의 왼쪽으로,
더 큰 값들은 오른쪽으로 몰아넣는다.
반환값은 피벗값의 최종 위치 인덱스이다.
"""
def swap(i: Index, j: Index) -> None:
"""
주어진 두 인덱스의 데이터를 서로 바꾼다.
"""
array[i], array[j] = array[j], array[i]
if low_idx != p_idx:
swap(low_idx, p_idx)
p_idx = low_idx
iter_idx = p_idx + 1
while iter_idx <= high_idx:
if array[p_idx] > array[iter_idx]:
swap(p_idx+1, iter_idx)
swap(p_idx, p_idx+1)
p_idx += 1
iter_idx += 1
return p_idx
recursive_qsort(0, len(array)-1)
return array
힙 정렬 (Heap sort)
우선순위 큐와 힙 문서 참조.
힙 자료구조로도 정렬을 할 수 있다. 먼저 정렬되지 않은 배열을 최대 이진 힙으로 구성한다. 그러면 가장 큰 수는 배열의 맨 처음에 위치할 것이다. 이 수를 추출하여 제거한 후, 이 빈자리를 힙의 맨 끝에 있는 숫자로 채운다. 물론 이 후 힙 순서 특성을 만족시키도록 힙을 재구성해주는 것도 잊지 말아야 한다. 그 후, 추출한 가장 큰 수를 배열의 맨 끝자리에 위치시킨다. 그러면 배열의 크기가 N일 때, 최대 이진 힙의 배열 내 범위는 인덱스 0부터 N-2까지이다. (여기서는 시작 인덱스를 0으로 잡았다) 이 과정을 힙에 남은 요소가 단 하나가 남을 때까지 반복하면 배열 내부는 자연스레 정렬이 될 것이다. 이 과정을 다음 예제에서 묘사해보았다. 소괄호는 최대 이진 힙의 범위이다.
원래 배열) [12, 5, 4, 8, 3, 9, 1, 10]
최대 이진 힙으로 구성) [(12, 10, 9, 8, 3, 4, 1, 5)]
[(5, 10, 9, 8, 3, 4, 1), 12]
[(10, 8, 9, 5, 3, 4, 1), 12]
[(1, 8, 9, 5, 3, 4), 10, 12]
[(9, 8, 4, 5, 3, 1), 10, 12]
[(1, 8, 4, 5, 3), 9, 10, 12]
[(8, 5, 4, 3, 1), 9, 10, 12]
[(1, 5, 4, 3), 8, 9, 10, 12]
[(5, 3, 4, 1), 8, 9, 10, 12]
[(1, 3, 4), 5, 8, 9, 10, 12]
[(4, 3, 1), 5, 8, 9, 10, 12]
[(1, 3), 4, 5, 8, 9, 10, 12]
[(3, 1), 4, 5, 8, 9, 10, 12]
[(1), 3, 4, 5, 8, 9, 10, 12]
[1, 3, 4, 5, 8, 9, 10, 12]
힙 정렬의 시간복잡도
먼저 기존 배열을 최대 이진 힙으로 만들어야 했다. 이 과정은 맨 처음에는 빈 힙부터 시작하여 하나씩 배열 내 요소들을 추가한 후, 추가할 때마다 힙 순서 특성을 만족시키도록 힙을 재구성하는 과정을 거친다. 힙을 재구성하는, 즉 힙을 구성하는 데이터들이 힙 순서 특성을 만족시키기 위해 자리바꿈하는 횟수를 구해야 한다.
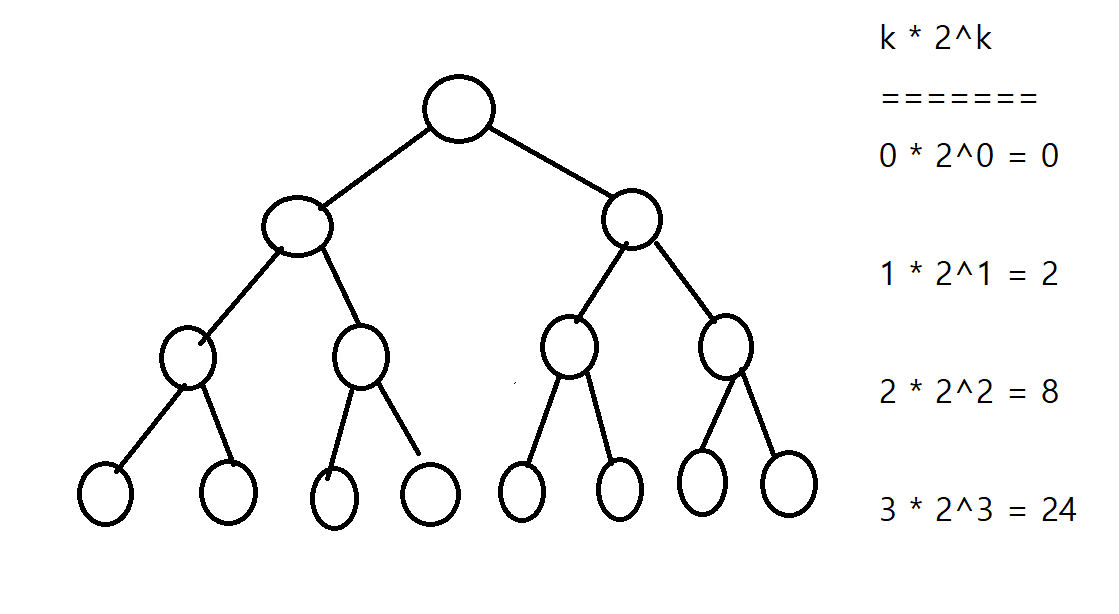
그림 2
그림 2를 보면 최악의 경우, 데이터를 하나씩 추가할 때마다 매번 자리를, 그것도 맨 마지막 데이터가 최상위층 데이터까지 바꿔야 한다. 그러면 N번째 데이터까지 힙에 추가한 경우 총 자리 바꿈한 횟수는 \(\sum_{i=0}^k i*2^i\)이다. 여기서 k는 힙의 높이다. 시간복잡도 \(O(k*2^k)\)를 구하면 다음과 같다.
\[k=log(N+1)-1 \\ N=2^{k+1}-1 \rightarrow 2^k =\frac{N+1}{2} \\ \therefore k*2^k=[log(N+1)-1](\frac{N+1}{2}) \\ \rightarrow NlogN\]즉, \(O(NlogN)\)이다.
힙을 정렬하는 동안에도 힙 내 요소가 하나씩 삭제될 때마다 재구성되어야 한다. 이에 대해서도 힙 재구성 시 자리바꿈 횟수를 구해보자. 시간복잡도를 구할 때는 결국에는 최고차항을 제외한 나머지 인수들은 생략되고, 최고차항의 계수도 생략되므로, 간단히 \(k = logN\)이라 표현하면, 힙 정렬 동안 힙 재구성 시 자리 바꿈 횟수는 다음과 같이 구할 수 있다.
\[log(N)+log(N-1)+...+log2 \\ = log(N!)\]위 식을 구하기 위해 스털링 근사(Stirling’s approximation)를 이용하겠다. 스털링 근사는 다음과 같다.
\[\ln(N!) \approx N\ln(N)-N\]-
스털링 근사 대략적인 유도
\[\begin{align*}\ln(N!) &= \ln[N(N-1)...3*2] \\ &= \ln(N)+\ln(N-1)+...+\ln2 \\ &=\sum_{k=1}^N\ln(k) \approx \int_{1}^N\ln(x)dx\end{align*}\]위 식의 마지막 부분은 N이 충분히 크다는 전제 하에 합을 적분으로 근사시켰다. 해당 적분을 구하면 다음과 같다.
\[부분\ 적분\ 적용)\ \begin{align*}\ &f = \ln(x),\ g'=1 \\ &f'=\frac{1}{x},\ g=x \end{align*}\] \[\begin{align*}\int_1^N\ln(x)dx&=[x\ln(x)]_1^N-\int_1^Ndx\\&=N\ln(N)-(N-1)\\&=N\ln(N)-N+1\\&\approx N\ln(N)-N\end{align*} \\ \therefore \ln(N!) \approx N\ln(N)-N\]마지막 줄은 N » 1이라는 가정하에 1을 제거한 것이다.
스털링 근사식을 우리가 구하고자 하는 자리 바꿈 횟수에 적용하면 다음과 같다.
\[\begin{align*} \log(N!)&=\frac{\ln(N!)}{\ln2} \\ &\approx \frac{N\ln(N)-N}{\ln2} \\ &=\frac{N[\ln(N)-1]}{\ln2} \\ &\rightarrow N\ln(N)\\&=N\frac{\log N}{\log e} \\ &\rightarrow N\log N \end{align*} \\ \therefore O(N\log N)\]이제, 처음 배열을 최대 이진 힙으로 구성할 때의 연산 횟수와 힙 정렬 동안의 연산 횟수를 합친 시간복잡도는 \(O(N\log N+N\log N)=O(2N\log N) =O(N\log N)\)임을 알 수 있다.
힙 정렬의 구현
def heap_sort(array: Array) -> Array:
"""
최대 이진 힙 (Max Binary Heap)을 이용하여 숫자가 들어간 배열을 정렬.
"""
N = len(array)
def swap(i: Index, j: Index) -> None: array[i], array[j] = array[j], array[i]
def is_less(i: Index, j: Index) -> bool: return array[i] < array[j]
def get_parent_idx(child_idx: Index) -> Index:
"""
최대 이진 힙의 자식 데이터의 부모 데이터 인덱스 반환.
"""
return ((child_idx-1) // 2)
def get_child_idx(parent_idx: Index, heap_end_idx: Index) \
-> tuple[Index | None, Index | None]:
"""
최대 이진 힙에서 부모 데이터의 두 자식 데이터 인덱스 반환.
자식 데이터가 존재하지 않으면 None으로 반환.
"""
lchild_idx = parent_idx * 2 + 1
rchild_idx = parent_idx * 2 + 2
if lchild_idx > heap_end_idx: lchild_idx = None
if rchild_idx > heap_end_idx: rchild_idx = None
return (lchild_idx, rchild_idx)
def go_up(child_idx: Index) -> None:
"""
힙 내 새 데이터 삽입 시 힙 재구성.
"""
parent_idx = get_parent_idx(child_idx)
while parent_idx >= 0:
if is_less(parent_idx, child_idx):
swap(parent_idx, child_idx)
child_idx = parent_idx
else: break
parent_idx = get_parent_idx(child_idx)
def go_down(heap_end_idx: Index) -> None:
"""
힙 내 최대값 추출 시 힙 재구성.
"""
target_idx = 0
lc_idx, rc_idx = get_child_idx(target_idx, heap_end_idx)
while lc_idx or rc_idx:
if rc_idx is None:
if is_less(target_idx, lc_idx):
swap(target_idx, lc_idx)
target_idx = lc_idx
break
if is_less(target_idx, lc_idx) or is_less(target_idx, lc_idx):
if is_less(lc_idx, rc_idx):
swap(target_idx, rc_idx)
target_idx = rc_idx
else:
swap(target_idx, lc_idx)
target_idx = lc_idx
lc_idx, rc_idx = get_child_idx(target_idx, heap_end_idx)
else: break
def make_max_binary_heap():
heap_end_idx = 0
while heap_end_idx < N:
go_up(heap_end_idx)
heap_end_idx += 1
def hsort(heap_end_idx: Index):
if heap_end_idx == 0: return
swap(0, heap_end_idx)
go_down(heap_end_idx-1)
hsort(heap_end_idx-1)
make_max_binary_heap()
hsort(N-1)
return array
Reference
[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)
[2] [알고리즘] 합병 정렬(merge sort)이란 - Heee’s Development Blog
[3] 알고리즘 | 합병정렬(Merge Sort) 시간복잡도 이해하기
[4] 퀵 정렬
[5] [알고리즘] 퀵 정렬(quick sort)이란 - Heee’s Development Blog
[6] build heap 시간복잡도 O(n) 이해하기
[7] 힙 정렬
[8] 스털링 근사
This content is licensed under
CC BY-NC 4.0


댓글남기기