[알고리즘][그래프] 그래프 개요

용어 정리

• node(vertex라고도 함): 꼭짓점, 정점. 정점의 개수를 N 또는 V라고 표기함.
• edge: 간선, 변. 노드와 노드를 잇는 선. 간선의 개수를 보통 E라고 표기함.
• degree: 차수. 한 꼭짓점에 연결된 변의 개수.
  • in-degree: 입력 차수. 한 꼭짓점으로 들어오는 변의 수.
  • out-degree: 출력 차수. 한 꼭짓점에서 나가는 변의 수.
• path: 경로. 한 꼭짓점에서 다른 꼭짓점으로 향하는 길이라고 보면 된다.
• adjacent matrix: 인접 행렬. 여러 개의 꼭짓점들과 변들로 이루어진 그래프에서, 특정 노드에서 다른 노드로 이어지는 변의 존재여부를 표시한 행렬.
• adjacent list: 인접 리스트. 어떤 노드와 그 노드로 향하는 인접한 노드들을 해시 테이블과 연결리스트 형태로 표현한 것.
• undirected graph: 무방향 그래프, 무향 그래프. 두 노드 u, v를 엣지로 연결할 때, u에서 v로도 이동 가능하고, v에서 u로도 이동 가능하게 연결한 그래프.
• directed graph: 방향 그래프, 유향 그래프. 두 노드 u, v를 엣지로 연결할 때 한 쪽 노드에서 다른 쪽 노드로는 이동 가능하나 그 반대는 불가능한 (즉, 일방통행) 그래프.
• weighted graph: 가중 그래프. 엣지에 가중치(weight)가 부여된 그래프. 가중치는 연결된 두 노드 사이의 관계를 표현한다. 가중치는 수치값으로 표현된다.

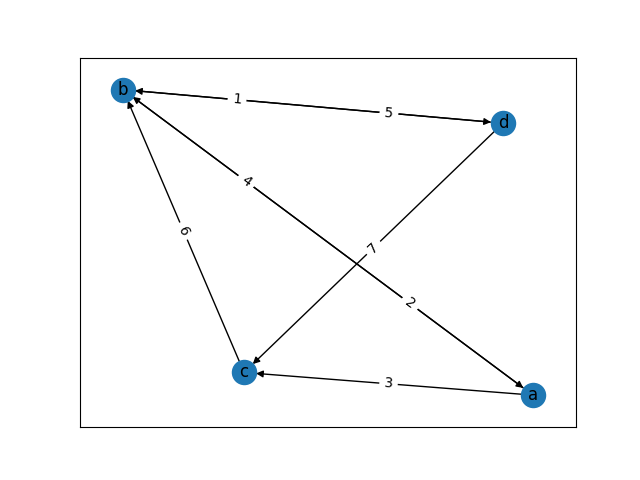
그림 1. 그래프의 예시. 위 그림은 weighted graph와 directed graph가 혼합되어 있다. (나중에 이런 그래프를 편의상 weighted-directed graph라고 부르겠다)

개요

그래프는 정보 또는 데이터를 엣지들로 연결된 노드들로 모델링한 것을 말한다. 그래프는 고유하게 식별할 수 있도록 label이 붙은 노드들에 대해, N개의 개별적인 노드들의 집합을 포함하는 자료형이다. 두 개의 노드를 연결하기 위해 엣지를 추가할 수 있다. 이 때 노드 u에서 노드 v로 연결한 엣지를 (u, v)라고 표현한다. 그리고 여기서 u, v는 각각 종점(endpoint)이라고도 한다. (u, v)에 대해서, u는 v에 인접(adjacent)하다고 하고, v도 u에 인접하다. (인접하다는 것은 두 노드가 중간에 다른 노드없이 직접 엣지로 연결되어있다는 뜻)

그래프에서, 엣지들로 연결된 노드들에 대해, 한 노드에서 다른 노드로 이동하는 것을 보행(walk)이라고 표현하기도 한다.

어떤 노드에서 다른 노드로 이동하고자 할 때, 시작점에 해당하는 노드를 source node라 하고, 종점에 해당하는 노드를 target node라 한다.

cycle(순환)은 시작점과 끝점이 동일한 경로(path)를 의미한다.

노드 u에서 노드 v로 향하는 경로가 존재할 때, 노드 v는 도달 가능(reachable)하다고 표현한다. 반대로, 노드 v로 향하는 경로가 하나도 존재하지 않을 때는 도달 가능하지 않다(unreachable)고 말한다. 도달 가능한 노드들로만 구성된 그래프를 연결 그래프(connected graph)라 하고, 도달 불가능한 노드가 존재하는 그래프를 비연결 그래프(disconnected graph)라 한다.

그래프의 모든 노드들이 다른 모든 노드들과 연결되어 있다면 이를 완전 그래프(complete graph)라고 한다. 이 때의 간선의 수는 전체 노드의 개수 n에 대해 \(\frac{n(n-1)}{2}\)개를 가진다.

그래프에는 다음과 같이 3가지 종류의 그래프가 존재한다.

• undirected graph: 무방향 그래프, 무향 그래프. 두 노드 u, v를 엣지로 연결할 때, u에서 v로도 이동 가능하고, v에서 u로도 이동 가능하게 연결한 그래프.
• directed graph: 방향 그래프, 유향 그래프. 두 노드 u, v를 엣지로 연결할 때 한 쪽 노드에서 다른 쪽 노드로는 이동 가능하나 그 반대는 불가능한 (즉, 일방통행) 그래프. 엣지는 보통 화살표로 표현한다.
• weighted graph: 가중 그래프. 엣지에 가중치(weight)가 부여된 그래프. 가중치는 연결된 두 노드 사이의 관계를 표현한다. 가중치는 수치값으로 표현된다.

그래프 관련 파이썬 외부 라이브러리

그래프를 표현해주는 내장 자료형이나 모듈이 파이썬에는 존재하지 않는다. 그래서 이를 직접 만들어 개발할 수도 있겠지만, 편리성을 위해 외부 라이브러리인 networkx 모듈을 사용하겠다. 해당 라이브러리가 설치되어 있지 않다면 터미널 창에서 다음을 입력하고 설치한다.

pip install networkx

해당 모듈을 이용한 그래프를 시각화할 때는 matplotlib이란 외부 라이브러리도 필요하니 설치되어 있지 않다면 pip install을 이용해 미리 설치하자. (다른 시각화 라이브러리들도 존재하겠지만 여기서는 그래프 시각화에 해당 모듈을 이용할 것이다)

다음은 networkx 모듈을 이용하여 그래프를 구성하는 예제 코드이다.

import networkx as nx

G = nx.Graph()  # undirected graph 생성.

# 노드는 None을 제외한 해시 가능한(즉, immutable한) 파이썬 객체라면 
# 모두 가능하다. 여기선 문자열로 채택하였다. 
G.add_node('A2') 
G.add_nodes_from(['A3', 'A4', 'A5'])  # 여러 노드들을 list로 동시에 추가.

G.add_edge('A2', 'A3') # 두 노드 사이의 edge 추가.

# 여러 edge들을 동시에 추가.
G.add_edges_from([('A3', 'A4'), ('A4', 'A5')])

for i in range(2, 6):
    # 만약 존재하지도 않는 노드 사이에 엣지를 추가하려고 시도하면 
    # 해당 노드들이 먼저 자동으로 추가되고 그 후에 엣지가 추가된다. 
    G.add_edge(f"B{i}", f"C{i}")
    if 2 < i < 5:
        G.add_edge(f"B{i}", f"B{i+1}")
    if i < 5:
        G.add_edge(f"C{i}", f"C{i+1}")

print(G.number_of_nodes(), "nodes.")  # 노드의 개수를 반환하는 메서드.
print(G.number_of_edges(), 'edges.')  # 엣지 개수 반환 메서드. 

# 'C3'과 인접한 노드를 반환.
print("adjacent nodes to C3: ", list(G['C3']))

# 'C3'과 인접한 엣지 반환. 
print("edges adjacent to C3: ", list(G.edges('C3')))

12 nodes.
12 edges.
adjacent nodes to C3:  ['C2', 'B3', 'C4']
edges adjacent to C3:  [('C3', 'C2'), ('C3', 'B3'), ('C3', 'C4')]

다음 페이지부터는 주로 그래프에서 특정 노드에서 다른 노드로 향하는 경로를 찾는 알고리즘들, 즉 그래프 탐색 알고리즘들에 대해 살펴볼 것이다.

---

References

[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)

[2]

파이썬 네트워크 시각화 분석하기(python networkx 예제) / 파이썬 데이터 분석 실무 테크닉 100

[3] networkx 외부 라이브러리 공식 문서.

Software for Complex Networks — NetworkX 3.1 documentation

[4]

[NetworkX] 그래프 종류 종합정리 (파이썬 네트워크 분석 5)

[5]

[NetworkX] 가중그래프, Weighted Graph (파이썬 네트워크 분석 2)

[6]

Weighted Graph — NetworkX 3.1 documentation

[7]

파이썬 networkx weight 추가 & 그리기

[8] 기존 그래프 위에 특정 경로를 표시하는 법.

n2_2_weighted_and_directed_graphs

[9] 두 가중치 값을 겹치지 않게 표시하는 법.

Phind: AI search engine

[10]

[NetworkX] 레이아웃으로 그래프 예쁘게 그리기 (nx layout)

[11]

그래프 이론 용어

[12]

그래프 이론 용어 우리말 번역 - Sang-il Oum (엄상일) (엄상일)

[13]

[알고리즘] 최단 경로 알고리즘 비교 및 사용 케이스 정리

[14]

Complete Graph – from Wolfram MathWorld

This content is licensed under CC BY-NC 4.0