[알고리즘][그래프] Weighted graph - Floyd-Warshall algorithm

2023-08-01 5 분 소요

All-pairs shortest path problemPermalink

Single source shortest path 문제에서는 정해진 source 노드로부터 임의의 노드까지의 최소 비용을 계산했었다. 반면 All-pairs shortest path 문제는 그래프 내 모든 한 쌍의 노드 사이의 누적 가중치를 구하는 문제이다. 즉, 그래프 내 모든 노드가 source 노드가 될 수 있는 것이다. 이번에는 All-pairs shortest path (줄여서 ASP라고 하겠다) 문제를 다루는 알고리즘에 대해 살펴보겠다.

Floyd-Warshall algorithmPermalink

접근법Permalink

해당 알고리즘에 대해 설명하기 전, ASP 문제에 접근하는 것에 대해 살펴보겠다.

이전의 거의 모든 그래프 탐색 알고리즘들이 그러했듯, 알고리즘 수행 과정에서 특정 노드 u에서 v로 향하는 최단 경로의 거리(최소 비용)를 기록하는 변수 (이 변수명을 dist_to라 하겠다)와 나중에 최단 경로를 구성하기 위해 종착 노드 v로 접근하는 바로 이전 노드를 저장하는 변수 (이 변수명을 node_from이라 하겠다) 이 두 가지가 필요했다. ASP 문제에 한해 좀 더 자세히 설명하면 다음과 같다.

dist_to 변수는 그래프 내 모든 한 쌍의 u, v 노드 사이의 최단 경로의 최소 비용을 기록하는 변수로, 2차원 구조체의 형태를 띤다. 예를 들면, u에서 v노드로 향하는 최단 경로의 최소 비용이 3이라면 dist_to[u][v] = 3이라고 하면 되겠다. 만약 u에서 v로 향하는 경로가 존재하지 않는다면 dist_to[u][v] = ∞으로 무한대로 정한다. 자기 자신으로의 최단 경로 거리는 0으로 설정한다. (dist_to[u][u] = 0) 파이썬에서는 해당 변수를 {a: {b: 3, c: 4, …}, …} 형식으로 딕셔너리 안의 딕셔너리 형태로 구현하면 되겠다.

node_from 변수는 그래프 내 두 노드 u, v에 대해 u에서 v로 향하는 최단 경로에서 v 노드의 바로 이전 노드를 value로 기록하는 변수로, 2차원 구조체의 형태를 띤다. 예를 들면, 두 노드 u, v로 향하는 최단 경로 사이에 아무런 노드도 존재하지 않고 u → v로 연결되어 있다면 node_from[u][v] = u로 지정한다. 만약 최단 경로 사이에 k라는 경로가 존재하여 u→k→v 경로가 된다면, node_from[u][v] = k라고 저장한다. (사실 이 경우, k = node_from[k][v]와도 같기에, node_from[u][v] = node_from[k][v]으로 값을 갱신해도 된다) 마찬가지로, 파이썬에서 구현할 때에는 {a: {b: a, c: d, …}, …} 형식으로, 딕셔너리 안의 딕셔너리 형태로 구현하면 되겠다.

위 두 변수 모두 인접 행렬을 사용해야함을 알 수 있다.

다음은 가중치 그래프와 이 그래프에 대한 두 변수를 인접행렬로 표현한 예이다.

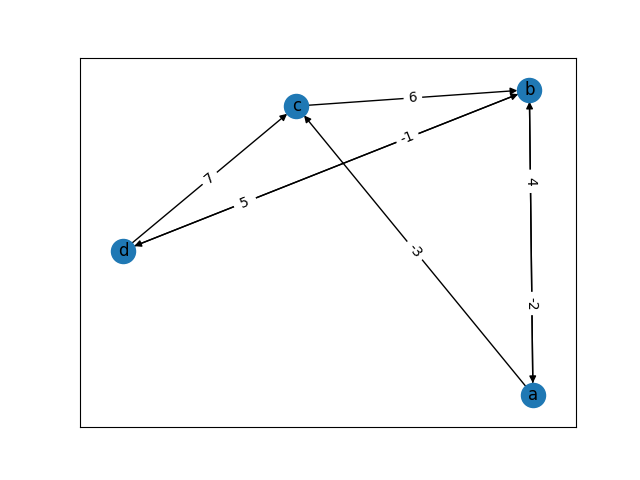
그림 1. 가중치 그래프의 예

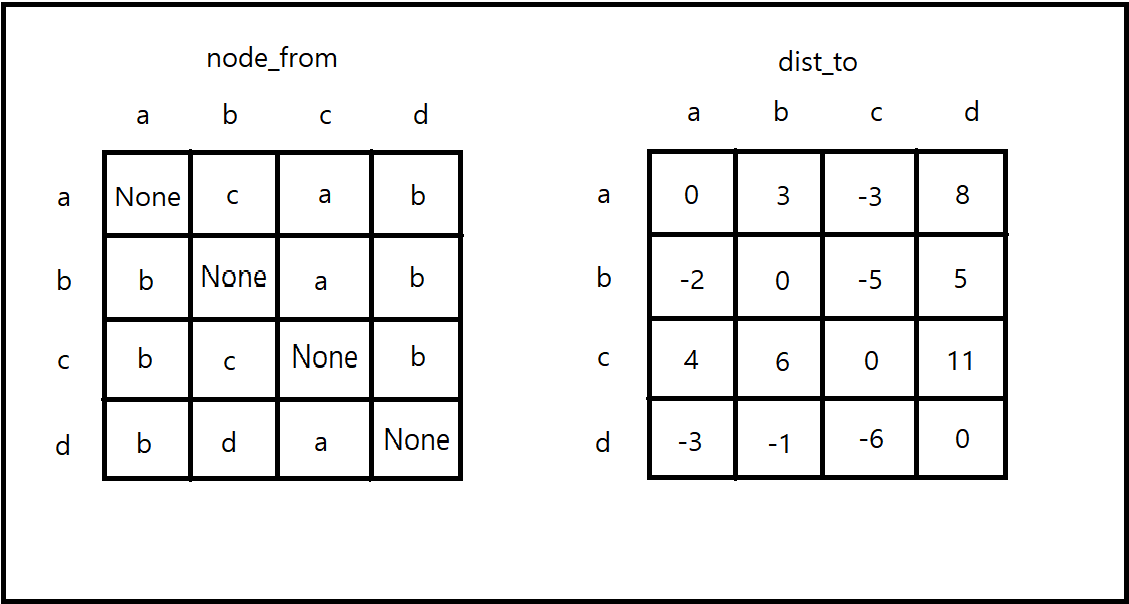
그림 2. 그림 1에 대한 두 변수를 인접행렬로 나타낸 모습

두 변수를 이용하여 임의의 두 노드 간의 최단 경로와 그 거리값을 알아내보자. 예를 들어 노드 a에서 노드 d까지의 최단 경로를 구하고자 한다. node_from 변수에서 node_from[a][d]를 통해 조회해보았다. 그 결과 그림 2를 보면 알겠지만, b가 나왔다. 이 말은, a에서 d로 향하는 최단 경로 사이에 노드 b가 존재한다는 뜻이다. 즉 a→b→d 순서대로 최단 경로가 생성된다는 것이다. 그런데 a와 b 사이에 또 다른 노드가 있을 수도 있다. 따라서 이번에는 node_from[a][b]를 조회한다. 그 결과 c가 나왔다. 즉, a에서 출발하여 노드 b로 향할 때 바로 이전에 노드 c가 존재한다는 것이다. 즉, a→c→b→d의 최단 경로를 거친다는 것이다. a에서 c 사이에 다른 노드가 존재하는지 확인하기 위해 node_from[a][c]를 검색해보면 a가 나온다. 즉, a와 c 사이에 또 다른 노드는 존재하지 않는다는 것이다. 따라서 결국 a에서 d로 가는 최단 경로는 a→c→b→d의 순서임을 알 수 있다. 이처럼, node_from 변수를 이용하여 최단 경로를 구성할 때 해당 변수 내에서 재귀적으로 검색하는 구조임을 알 수 있다.

알고리즘 원리와 코드 구현Permalink

이제 본격적으로 Floyd-Warshall 알고리즘에 대해 살펴보겠다. 앞서 살펴보았듯, 두 노드 u, v에 대해, u에서 v로 향하는 최단 경로는 u→v와 같이 u에서 v로 직접 이어지는 경로가 아닌 중간 노드 k를 경유하는 u→k→v 경로가 최단 경로가 될 수 있다. 따라서 모든 노드에 대해서 dist_to[u][k] + dist_to[k][v] < dist_to[u][v]인지를 확인하고, 맞으면 최단 경로와 그 거리를 갱신해줘야한다. 그렇기에 해당 알고리즘을 코드로 구현할 때 삼중 for문이 필요하다.

해당 알고리즘을 코드로 구현하기 전, 다음의 클래스를 정의하였다. 다음의 코드는 앞선 Weighted graph - Dijkstra algorithm 문서의 예제로 보았던 모듈에 이어서 작성하였다.

class AllPairShortestPath():
    """
    weighted graph에서 가중치를 고려하여 임의의 두 노드 u, v에 대해 
    u에서 v로 향하는 최단 거리와 그 경로를 구하는 알고리즘 클래스. 
    Single node shortest path 문제에서는 source 노드라는 시작점이 정해진 
    것에 비해, 이 문제는 어떤 두 노드를 임의로 고르더라도 두 노드 간 최단 
    거리 및 경로를 구한다는 차이점이 존재. 
    """
    def __init__(
            self, 
            graph_inst: nx.Graph | nx.DiGraph,
            source_node: Node,
            target_node: Node
        ):
        self.graph = graph_inst
        self.src = source_node
        self.tar = target_node
        self.dist_to: dict[Node, dict[Node, Distance]] = {}
        self.node_from: dict[Node, dict[Node, Node | None]] = {}

    def resetAttr(self) -> (None):
        """
        self.dist_to, self.node_from 등의 인스턴스 속성들을 리셋한다. 
        """
        self.dist_to.clear()
        self.node_from.clear()

다음은 Floyd-Warshall 알고리즘을 코드로 구현한 것으로, 위 예제 1-1에 이어 인스턴스 메서드로 작성하면 된다.

def floydWarshallAlgorithm(self) -> (None):
        self.resetAttr()
        for u in self.graph.nodes():
            self.dist_to[u] = {v:INF for v in self.graph.nodes()}  #2
            self.node_from[u] = {v:None for v in self.graph.nodes()}  #3
            self.dist_to[u][u] = 0  #4  # 자기 자신 노드로의 거리는 0으로 설정.
            for e in self.graph.edges(u, data=True):  #5
                v = e[1]
                # 처음 u -> v 거리는 두 노드 사이의 edge의 가중치로 초기화.
                self.dist_to[u][v] = e[2]["weight"]
                # u -> v로 최단 거리로 향할 때 v 노드로 향하는 이전
                # 노드를 u로 초기화.
                self.node_from[u][v] = u  #6
        
        for k in self.graph.nodes():
            for u in self.graph.nodes():
                for v in self.graph.nodes():
                    shortest_dist = self.dist_to[u][k] + self.dist_to[k][v] #7
                    if shortest_dist < self.dist_to[u][v]:
                        # u -> v로 곧장 가는 것보다 u -> k -> v로 가는 것이 
                        # 더 빠를 경우. 
                        self.dist_to[u][v] = shortest_dist  #8
                        # u -> v로 향할 때 v로 향하는 이전 노드를 
                        # k -> v로 향할 때 v로 향하는 이전 노드로 업데이트.
                        # 예) u -> k -> v일 경우,
                        # node_from[u][v] = node_from[k][v] = k
                        self.node_from[u][v] = self.node_from[k][v]

다음은 위 예제 1-2의 메서드를 통해 얻은 dist_to, node_from 변수들의 정보를 토대로 각각 특정 노드 u에서 v로의 최단 경로를 구성하는 메서드와 그 최단 경로의 거리값을 구하는 메서드를 이어서 작성한 것이다.

def reconstructAllPairsPath(self) -> (list[Node]):
        """
        floydWarshallAlgorithm을 통해 얻은 정보를 통해 
        source 노드로부터 target 노드까지의 최단 경로를 구하고 이를 반환. 
        """
        if self.node_from[self.src][self.tar] is None:
            error_msg = f"""Error from the instance method 
            reconstructAllPairsPath() in class AllPairShortestPath. 
            the path from source node {self.src} to target node {self.tar} is 
            unreachable."""
            raise ValueError(error_msg)
        path = []
        v = self.tar
        while v != self.src:
            path.append(v)
            v = self.node_from[self.src][v]
        path.append(self.src)
        path.reverse()
        return path

    def getShortestDistance(self) -> (Distance):
        """
        src 노드부터 tar 노드로 향하는 최단 경로의 거리를 반환.
        """
        return self.dist_to[self.src][self.tar]

시간복잡도Permalink

앞서 예제 1-2를 보면 알 수 있듯, 삼중 for문을 사용하는 것을 볼 수 있다. 즉, 그래프 내 전체 노드의 개수 N에 대해, $O(N^3)$ 의 시간복잡도를 가진다.

사실 Floyd-Warshall 알고리즘은 그래프 내 모든 N개의 노드들에 대해서, 각 노드를 탐색 시작점으로 하여 총 N번동안 다익스트라 알고리즘을 수행한 것과도 같다. 앞서 다익스트라 알고리즘을 인접행렬로 구현하면 시간복잡도는 $O(N^2)$ 인 것을 확인하였다. 이를 N개의 모든 노드에 대해서 실행하는 것과 같으므로 $N*O(N^2)=O(N^3)$ 으로 귀결된다.