[알고리즘] 동적 계획법 (Dynamic Programming)

피보나치 수열은 다음과 같은 형태를 띤다.

0 1 1 2 3 5 8 13 21, ...

특정 항의 값을 구하려면 그 이전의 두 항의 값들을 합치면 된다. 0 + 1 = 1, 5 + 8 = 13 이렇게 말이다. 이를 조금 더 수학적으로 표현하면 다음과 같다.

F(0) = 0  (n = 0부터 시작)
F(1) = 1
F(n) = F(n-1) + F(n-2) (n > 1)

위와 같이 점화식 형태를 띤다. 그렇다면 이를 코드로 어떻게 구현할 수 있을까?

예를 들어, F(5) = F(4) + F(3)이고, F(4) = F(3) + F(2) 이다. 즉, 큰 문제를 좀 더 작은 문제로 나누어 푸는 형태이며, 마치 트리 자료구조에서 하위 트리로 계속해서 나아가는 형태이다. 이러한 형태를 재귀 함수로 풀 수 있을 것 같다. 그래서 재귀 함수를 이용하여 다음과 같이 구현해보았다.

def fibo_recur(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    
    return fibo_recur(n-1) + fibo_recur(n-2)

예제 1-1

매개변수 n에 여러 자연수를 대입하여 실행해본 결과, 정확히 나오는 것으로 확인되었다. 그러나 문제는 입력값인 n의 크기가 조금만 커져도 구하는 시간이 오래 걸린다는 것이다. 실제로 n = 40을 대입했을 때 해당 함수의 실행 시간을 재보니 약 3분이 걸렸다. 이 정도면 꽤 긴 시간이라 생각된다. (처음 실행할 때 프로그램이 어떤 오류로 인해 비정상적으로 멈춘 줄로 착각할 정도였다)

그렇다면 이렇게 재귀 함수를 이용하여 피보나치 함수를 구현했을 때, 입력값이 조금만 커져도 왜 이리 실행 시간이 오래 걸리는 것일까? 우선 다시 피보나치 개념으로 돌아가보자. 예를 들어 F(5)를 구한다고 가정해보자.

F(5) = F(4) + F(3)
F(5) 우항의 왼쪽 항 구하기: F(4) = F(3) + F(2)
F(5) 우항의 오른쪽 항 구하기: F(3) = F(2) + F(1)  (중복)
F(4) 우항의 왼쪽 항 구하기: F(3) = F(2) + F(1)  (중복)
F(4) 우항의 오른쪽 항 구하기: F(2) = F(1) + F(0) (중복)
F(3) 우항의 왼쪽 항 구하기: F(2) = F(1) + F(0) = 1 + 0 = 1 (중복)
(이하 생략)

F(5)라는 비교적 작은 수를 대상으로 피보나치 수를 구하는 과정인데도 중간 과정에서 중복된 계산이 꽤 많은 것을 알 수 있다. 이 중복되는 계산을 마주칠 때마다 일일이 계산하도록 하였기 때문에 시간이 많이 걸린 것이다. F(5)를 구하는 과정을 그래프로 그려보면 다음과 같다.

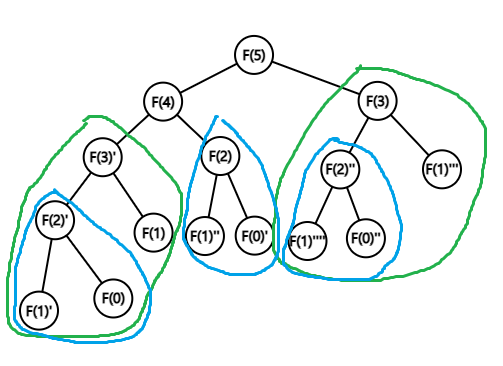
그림 1. 피보나치 수 F(5)를 구하는 과정을 그래프로 나타낸 그림. 중복되는 계산 과정을 색상별로 표현하였다.

위 그림을 보면 알겠지만, 하위 문제로 나누고 이를 해결하는 과정에서 중복되는 계산 부분이 꽤 많다는 것을 알 수 있다. 위 그래프는 이진 트리와도 그 구조가 똑같은 것을 알 수 있다. 이진 트리와 같은 구조를 가지는 트리는 그 노드 수가 보통 2^N개이다. 따라서 위와 같이 자식 노드의 수가 항상 2개 이하로 나눠지는 문제의 경우 이를 단순히 재귀 함수 형태로 푸는 방식은 \(O(2^N)\)의 시간복잡도를 가지게 된다고 볼 수 있다. 이는 꽤 비효율적이다. 앞서 예를 든 F(40)을 구하려면 2^40 = 1,099,511,627,776 번의 연산이라는 어마어마한 연산 횟수가 필요로 한다는 것이다.

그렇다면 이러한 비효율적인 문제를 어떻게 해결할 수 있을까? 이에 대한 대안으로 동적 계획법(Dynamic programming)이란 것이 존재한다.

동적 계획법

위 피보나치 수 문제를 자세히 보면 다음의 특징이 있음을 알 수 있다.

• 전체 문제를 하위 문제들로 쪼갠 후, 각 하위 문제들을 먼저 해결하는 방식이다. 이는 분할 정복 방식과 매우 흡사하다.
• 하위 문제들로 분할 했을 때, 여러 하위 문제들의 계산이 서로 중복되는 경우가 많다.

동적 계획법은 이렇게 전체 문제를 여러 개의 하위 문제로 분할하였을 때, 하위 문제들의 결과값들이 여러 번 중복되면 계산은 한 번만 하고 이를 따로 저장한 뒤, 중복되는 계산이 요구될 때 또 똑같은 계산을 하지 않고 이미 저장된 계산 결과를 가져다 쓰도록 하여 성능적으로 최적화를 꾀한 알고리즘이다. 이 동적 계획법에 따르면, 피보나치 수를 구현하는 함수를 작성할 때, F(0), F(1), F(2), F(3) 등의 하위 문제들의 계산 결과값을 처음 한 번만 계산한 뒤, 이를 메모리에 저장하고, 나중에 또 같은 계산을 요구하면 메모리에서 그 결과값을 꺼내 사용하도록 하는 방식이다. 그러면 중복 계산 과정이 사라지기에 앞서 보인 단순한 재귀 함수 방식보다 시간적으로 더 효율이 있다.

어떤 문제가 동적 계획법을 적용하기에 적절한 문제인지는 다음의 두 단서를 모두 만족하면 적용시킬 수 있다.

• 최적 부분 구조 (Optimal substructure) : 전체 문제의 최적해는 그 부분 문제들의 최적해들로부터 구할 수 있어야 한다.
• 중복 부분 문제 (Overlapping subproblems) : 전체 문제를 여러 개의 하위 문제들로 분할하였을 때, 하위 문제들의 최적해를 구하는 계산이 여러 번 중복될 때.

앞서 예를 든 피보나치 수열은 위 두 조건을 모두 만족시킨다. F(5)는 F(4), F(3) 등의 하위 문제들을 풂으로써 그 값을 알아낼 수 있는 구조이며, 그 과정에서 여러 하위 문제들의 계산이 서로 중복되는 특징을 가지고 있다.

top-down VS bottom-up

동적 계획법을 통해 문제를 풀 때, 두 가지 방식으로 풀 수 있다. 하나는 top-down 방식으로, 전체 문제에서 먼저 시작하여 분할된 여러 하위 문제들을 상위 레벨부터 시작하여 점점 하위 레벨에 있는 하위 문제들로 전진하여 푼 다음, 하위 문제들로부터 나온 해들을 토대로 전체 문제를 푸는 방식이다(앞서 제시한 트리 그래프를 떠올리면, 맨 위에 있는 루트 노드부터 시작하여 리프 노드를 향해 아래로 한 층씩 내려가는 구조이다). 이 때 중복되는 계산 결과는 미리 저장했다가 이 저장된 데이터를 활용하는 방식이다. 계산 결과를 “메모(memo)”하면서 푼다는 의미에서, 이렇게 계산 결과를 기록하고 이후 중복되는 계산에 대해 저장한 결과를 이용하는 기법을 메모이제이션(memoization)이라고 한다. (메모리제이션(memorization)이 아니니 헷갈리지 말도록 하자) 캐시(cache)와도 같다.

다음은 피보나치 수열을 top-down 방식의 동적 계획법으로 구현한 예제이다.

def fibo_dp_top_down(n, memo={}):
    if n in memo:
        return memo[n]
    
    if n <= 1:
        memo[n] = n
    else:
        memo[n] = fibo_dp_top_down(n-1, memo) + fibo_dp_top_down(n-2, memo)
    return memo[n]

예제 2-1

보통 top-down 방식에는 재귀 호출 방식을 사용한다. 따라서 재귀 호출이 너무 많아지면 스택 메모리를 과도하게 잡아먹고, 결국에는 정해진 스택 메모리를 초과하는 stack overflow 현상이 발생할 수 있다는 단점이 있다. 다만, 바로 뒤에 나올 bottom-up 방식에서 모든 가능한 하위 문제들을 계산하여 그 모든 값을 저장하는 방식인 tabulation과 비교하면 메모이제이션 기법은 실제로 하위 문제들을 계산하는 도중 마주치는 계산에 대해서만 그 결과값을 저장하기에 이 방식과 비교하면 상대적으로 연산 횟수도 적고, 차지하는 메모리 양도 적은 장점을 가진다.

bottom-up 방식은 top-down 방식과 반대로 분할된 하위 문제들부터 먼저 푼 다음에 전체 문제를 해결하는 방식이다(앞서 본 트리 그래프를 예로 들면, 맨 아래층의 리프 노드들부터 시작하여 루트 노드를 향해 한 단계씩 위로 올라가는 구조라 보면 된다). 이 방식에서 사용되는 계산 결과 저장 방식은 tabulation(표) 기법을 사용한다. 메모이제이션과의 차이점은, 메모이제이션은 마주치는 하위 문제들의 계산에 대한 결과값만을 저장하는 느긋한 연산(lazy-evaluation) 방법을 사용한다. 즉, 필요한 연산 결과만을 저장한다. 반면, 타뷸레이션 기법은 불필요할 수도 있는 연산까지도 다 미리 계산하여 저장한다는 것이 차이점이다. 따라서 bottom-up 방식은 불필요한 연산에 의해 top-down 방식에 비해 성능이 조금 더 안 좋을 수 있고, 상대적으로 메모리도 더 차지한다는 단점이 있다. 반면 bottom-up 방식은 재귀 함수 방식이 아닌 iteration, 즉 순회 방식을 사용한다. 따라서 호출 스택에 대한 overflow 현상은 걱정하지 않아도 된다.

다음은 bottom-up 방식의 동적계획법을 사용하여 피보나치 수를 구현한 예제이다.

def fibo_dp_bottom_up(n):
    # 피보나치 수열을 n = 0부터 시작함.
    memo = [0, 1] + [0] * (n-1)

    for i in range(2, n+1):
        memo[i] = memo[i-1] + memo[i-2]
    
    return memo[n]

예제 2-2

위 예제를 보면 알 수 있듯, bottom-up 방식의 동적계획법에는 재귀호출 대신 for문을 이용한 iteration 방식을 사용한다는 것을 알 수 있다.

시간복잡도

앞서 피보나치 수를 예로 든 동적계획법을 살펴보면, 단순한 재귀호출 방식은 모든 하위 문제들을 중복되는 것이 있더라도 모두 계산하는 특성상 그 시간복잡도가 \(O(2^N)\)으로, 입력값 N의 크기가 커지면 연산 횟수가 지수적으로 급증하는 형태인 반면, 동적계획법은 메모이제이션을 사용하기에 F(5)의 경우 F(4), F(3), F(2), F(1), F(0)만 계산하면 된다. 즉, 동적계획법은 입력값 N에 대해 시간복잡도 O(N)을 가진다는 것을 알 수 있다. 반면 단순 재귀호출 방식은 재귀호출에 의한 호출 스택 메모리를 사용하지만, 그 외의 다른 메모리를 사용하지는 않는다. 그러나 동적계획법은 메모이제이션을 위해 O(N)에 해당하는 메모리들을 따로 할당하여 사용한다는 특징이 있다. 동적계획법은 공간적인 특성에서는 조금 불리할지도 모르나, 그만큼 시간복잡도를 개선하는 알고리즘이다. 즉 어떻게 보면 공간과 시간을 맞바꾸는 알고리즘이라고도 볼 수 있다.

실제 성능 비교

정말로 동적 계획법을 이용하여 피보나치 수를 구하는 함수를 구현하는 방식과 단순 재귀 호출 방식 간의 성능적 차이가 있는지 확인해보겠다. 먼저, 어떤 함수를 실행할 때 그 실행 시간을 측정해주는 데코레이터를 다음과 같이 정의하였다.

def count_time(func):
    def inner(*args, **kwargs):
        start = time.time()
        result = func(*args, **kwargs)
        end = time.time()
        return (result, end - start)
    
    return inner

예제 3-1

그리고 그 아래에 다음의 코드를 준비하였다.

if __name__ == '__main__':
    target = 40

    def print_result_with_time(func_list):
        for func in func_list:
            exec_func = count_time(func)
            result = exec_func(target)
            print(f"결과: {result[0]}  - 시간 : {result[1]}")

    print_result_with_time([fibo_recur])
    print_result_with_time([fibo_dp_top_down, fibo_dp_bottom_up])

예제 3-2

앞서 구현한 피보나치 함수들을 토대로 위 코드를 실행해보면 입력값 n = 40일 때 다음의 결과를 얻는다.

결과: 102334155  - 시간 : 188.68918347358704
결과: 102334155  - 시간 : 0.0009472370147705078
결과: 102334155  - 시간 : 0.0

예제 3-1~2 실행결과

단순 재귀 호출을 이용한 방식은 188초, 그러니까 약 3분이 소요되는 반면, 각각 top-down과 bottom-up 방식의 동적계획법을 이용한 함수는 그 실행시간이 거의 0초가 걸리는 것을 확인할 수 있다. 이를 통해, 동적 계획법의 성능이 상대적으로 훨씬 좋다는 것을 알 수 있다.

이 페이지에서 선보인 코드들의 소스 코드는 다음의 링크를 참조. https://github.com/JeroCaller/ds-and-algo-in-python/blob/main/algorithms/dynamic_programming.py

---

References

[1] [Algorithm] Dynamic Programming (동적 계획법)

[2] 동적 프로그래밍 (Dynamic Programming, DP)

[3] 동적 계획법

[4] 메모이제이션

This content is licensed under CC BY-NC 4.0