[알고리즘][그래프] Weighted graph - Dijkstra algorithm
개요
가중치 그래프에서 가중치는 edge에 부여한다. 이러한 가중치는 무방향, 방향 그래프 모두에 쓰일 수 있다. 가중치라는 것은 수치적으로 부여하며, 양수, 0, 음의 정수가 될 수 있다.
지도에서 어떤 지점에서 다른 지점으로 가는 거리를 그래프로 모델링할 때, 특정 지점을 노드, 그 노드 사이를 잇는 도로를 edge, 두 지점 간 거리를 가중치로 할 수 있다.
가중치 그래프의 경우, source 노드부터 target 노드까지 가는 최단 경로를 찾아내는데에 이전에 다뤘던 알고리즘들을 대입할 수는 없다. 노드에서 노드로 향할 때 건너게 되는 노드의 개수가 최소인 경로가 최단경로가 아니라, 중간에 건너게 되는 간선들의 가중치들의 합이 최소인 경로가 최단경로가 되기 때문이다. 즉, 가중치를 고려해야한다.
source 노드로부터 특정 노드로 향하는 최단 경로를 구하는 문제를 Single-source shortest path 문제라 한다. (단일 출발지 최단 경로 문제라고 해석할 수 있겠다) 반면, source 노드는 주어지지 않은 채, 그래프 내 임의의 두 노드 간의 최단 경로를 구하는 문제를 all-pairs shortest path 문제 (모든 쌍의 최단 경로)라고 한다.
지금부터는 가중치 그래프 내 두 노드 간 경로 또는 최단 경로를 탐색하는 알고리즘들에 대해 살펴보겠다. 그리고 다음의 설명들은 마치 길찾기 문제처럼, 가중치를 노드와 노드 사이로 도달하는 데에 걸리는 거리값이라고 간주하겠다. (가중치 그래프로 모델링할 수 있는 모든 문제가 길찾기와 같은 문제가 아니므로 일반적으로는 “거리값” 대신 “비용값”이란 용어를 쓰는 게 더 적절한 것 같다)
Dijkstra Algorithm (다익스트라 알고리즘)
다익스트라 알고리즘은 가중치 그래프에서 single-source shortest path 문제를 풀 수 있는 알고리즘 중 하나이다. 해당 알고리즘을 사용하기 위해서는 그래프 내 모든 가중치가 하나도 빠짐없이 0 또는 양수여야 한다.
해당 알고리즘을 코드로 구현하기 위해서는 두 가지 변수가 필요하다. 하나는 source 노드로부터 target 노드까지의 최단경로의 거리를 기록하는 변수이다. 이 변수를 dist_to라 한다면, target 노드 v에 대해서 dist_to = {v: 10, w: 14}의 형태를 지니도록 한다. 해당 변수 안에 key로 들어간 값들은 모두 도착 노드들이다. 즉, source 노드로부터 v 노드까지 가는 최단 경로의 거리가 10이다, 라는 뜻이다. 또 하나의 변수는 탐색 과정에서 후에 최단 경로를 구성하기 위해 필요한 변수이다. 해당 변수를 edge_to라고 한다면, edge_to = {v: (n, v)}의 형태를 띈다. 즉, 특정 노드를 key로 하고, 그 노드로 향하는 이전 노드들 중 최단 경로를 구성하는 노드를 edge 형태로 value에 저장하는 방식이다.
다익스트라 알고리즘의 내용은 다음과 같다. 처음에는 source 노드로부터 다른 노드까지의 거리를 모두 무한대 (infinity)로 설정한다. 여기서 source 노드에서 source 노드로 가는 거리는 0으로 설정한다. 그 후, source 노드부터 시작하여 해당 노드에 연결된 간선들과 노드부터 탐색한다. source 노드와 연결된 간선의 가중치와 해당 간선으로 연결된 노드 v에 기록된 거리값을 비교한다. 처음에는 source 노드를 제외한 모든 노드들의 거리값이 무한대로 저장되어있으므로 이 때에는 항상 source 노드의 거리값 + 가중치의 값이 더 작다. 이 경우, 해당값을 노드 v의 거리값으로 업데이트한다. 이러한 과정을 source 노드에 연결된 모든 간선에 대해 실행한 후, 이번에는 다른 노드로 넘어가 같은 과정을 반복한다. 이 과정은 모든 노드들이 겪도록 해준다. 해당 과정에서, 특정 노드 v로 향하는 거리값이 이미 계산된 경우, 노드 v로 향하는 기존 경로의 거리보다 새로 탐색하는 경로의 가중치 + 이전 노드의 거리값이 더 작은 경우, 노드 v의 거리값이 해당값으로 새로 갱신되게끔 하기에 결국 최단 경로를 찾을 수 있게 된다.
다음은 위 과정을 그래프로 표현한 모습이다.
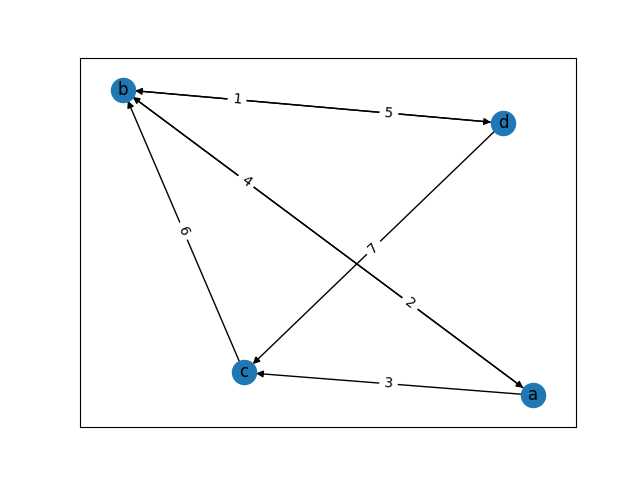
그림 1-1. weighted-directed graph 예시
그림 1-2. 다익스트라 알고리즘 초기 과정. a 노드를 source 노드로 가정하여 해당 노드의 거리값을 0으로 하고, 나머지 노드들의 거리값을 무한대로 설정한다.
그림 1-3. source 노드인 a 노드에 연결된 노드들의 거리값을 직접 연결된 간선들의 가중치를 이용하여 계산하고 갱신하는 과정. 현재 a 노드와 연결된 노드에 대해서만 진행하였으므로 노드 d의 거리값은 갱신되지 않는다.
그림 1-4. a 노드에서의 알고리즘 처리 과정이 끝난 후, c 노드로 옮겨 같은 과정을 반복한 후, 그 다음 b 노드로 옮겨 같은 과정을 진행하는 모습. c 노드에서 인접한 노드들의 거리값 계산에 갱신 과정이 없어서 이를 생략하여 표현하였다. b 노드에는 d 노드로 향하는 간선이 있어 d 노드의 거리값도 계산되어 갱신되었다. 이후, d 노드에 대해서도 진행하면 거리값이 새로 갱신되지 않아 사실 위 그림이 최종 결과이다.
위 그림에서 노드 c의 거리값을 계산하는 과정이 2번 정도 나타난다. 맨 처음 a 노드부터 시작하여 해당 노드의 거리값을 계산하면 3이다. 나중에 d 노드로부터 c 노드의 거리값을 계산하면, d 노드의 거리값인 9와 간선 (d, c)의 가중치 7을 합쳐 16이 된다. 그러나 이는 c 노드의 거리값 3보다 크므로 c 노드의 거리값이 갱신되지 않는다. 만약 처음 c 노드의 거리값이 예를 들어 20이었다면, d 노드로부터의 거리 계산에서 16이 20보다 작으므로 해당 노드의 거리값은 16으로 새로 갱신되었을 것이다.
다익스트라 알고리즘을 코드로 구현하기에 앞서 다음과 같이 먼저 코드를 작성하였다.
import networkx as nx
import matplotlib.pyplot as plt
from typing import final
# type alias
Value = object
Priority = int
Index = int
Node = object
Edge = tuple[Node, Node]
Distance = int
Weight = int
# 상수 정의
INF: final = float('inf')
그 후, 다익스트라 알고리즘을 구현하는 클래스와 메서드를 다음과 같이 구현하였다.
class SingleNodeShortestPath():
"""
weighted graph에서 가중치를 고려하여 source 노드에서 특정 노드까지의
최단 거리 및 해당 경로를 찾는 알고리즘 모음.
"""
def __init__(
self,
graph_inst: nx.Graph | nx.DiGraph,
source_node: Node,
target_node: Node
):
self.graph = graph_inst
self.src = source_node
self.tar = target_node
self.dist_to: dict[Node, Distance] = {}
self.edge_to: dict[Node, Edge] = {}
다익스트라 알고리즘을 구현하기 위해서는 indexed min priority queue (인덱스 최소 우선순위 큐)라는 자료구조를 먼저 구현해야 한다. 해당 자료구조는 priority queue와 거의 다를 바 없으나, 차이점은 말 그대로 우선순위 큐에 존재하는 값들을 index로 참조하는 방식이기에, 우선순위 큐 내에 존재하는 값들과 우선순위를 key-value 쌍 데이터로 하는 해시테이블로 저장하면 특정 값을 조회하는 데에 시간복잡도가 O(1)이다(파이썬의 dictionary 자료형이 해시테이블을 이용한 자료형이기에 해당 자료형을 사용할 것이다). 기존의 priority queue 자료구조를 이용하면 해당 자료구조 내에 있는 특정 데이터를 조회하기 위해서는 최악의 경우 모든 N개의 데이터들을 다 조사해야 하기 때문에 해당 연산의 시간복잡도는 O(N)이 된다. 이러한 단점을 극복하기 위해 index라는 개념을 쓰는 것이다.
다익스트라 알고리즘에 쓰일 해당 자료구조의 또 하나의 차이점은 특정 데이터의 우선순위 수치값을 원하는 값으로 감소시키는 기능을 하는 메서드 decreasePriority가 존재한다는 것이다. 그래프 내 노드가 value가 되고, 각 노드들의 거리값이 priority가 되는 방식인데, 앞서 설명했듯 각 노드들의 거리값을 계산하면서 더 작은 거리값이 계산되면 이를 갱신해줘야한다. 이러한 기능을 하는 것이 바로 decreasePriority 메서드이다.
해당 알고리즘은 우선순위 큐를 사용하기에, 매번 거리값이 갱신될 때마다 거리값이 더 작은 노드를 기준으로 먼저 계산하도록 하는 구조를 지닌다.
다음은 indexed min priority queue를 구현하는 코드이다. 예제 1-1의 바로 아래에 작성하였다.
class IndexedMinPQ():
def __init__(self):
self.N = 0
self.values: list[Value] = [None]
self.priorities: list[Priority] = [None]
# value들을 모은 리스트에 각각의 value들이 해당
# 리스트의 어느 인덱스에 존재하는지를 기록하기 위해
# 각 value에 해당하는 index를 저장하는 변수.
# 해당 변수의 존재로, 특정 value를 O(1)만에 찾을 수 있음.
# dictionary는 hashtable로 구성되어있기 때문.
self.location: dict[Value, Index] = {}
def getCurrentSize(self) -> (int):
"""
현재 힙 내에 저장된 데이터의 수 반환
"""
return self.N
def peek(self) -> (tuple[Value, Priority] | tuple[None, None]):
"""
제일 먼저 출력될 아이템의 value와 priority를 반환.
"""
if self.N == 0:
return None, None
v = self.values[1]
p = self.priorities[1]
return v, p
def isEmpty(self) -> (bool):
"""
우선순위 큐가 비어있는지 확인하는 메서드. 비어있으면 True 반환.
"""
return self.N == 0
def __contains__(self, target_value: Value) -> (bool):
"""
각 value의 리스트 내 인덱스 위치를 기록하는 변수
self.location의 존재 덕분에 O(1)이라는 짧은 시간 내에
해당 값이 우선순위 큐에 존재하는지 확인할 수 있다.
"""
return target_value in self.location
def _less(self, i: Index, j: Index) -> (bool | None):
"""
두 인덱스에 해당하는 value들의 우선순위를 비교하여
i의 우선순위가 j의 것보다 더 작은지를 확인하는 메서드.
우선순위의 수치값이 작은 value가 더 우선순위가 높은 구조를 가지는
우선순위 큐이기에 i > j이면 True, 그렇지 않으면 False 반환.
매개변수로 입력받은 두 인덱스 중 하나라도 None이라면 None을 반환.
"""
if (i is None) or (j is None): return None
return self.priorities[i] > self.priorities[j]
def _swap(self, i: Index, j: Index) -> (None):
"""
주어진 두 인덱스 i, j에 해당하는 두 개체의 위치를 바꾼다.
"""
self.values[i], self.values[j] = self.values[j], self.values[i]
self.priorities[i], self.priorities[j] = \
self.priorities[j], self.priorities[i]
self.location[self.values[i]] = i
self.location[self.values[j]] = j
def _getParentIndex(self, child_index: Index) -> (Index | None):
"""
힙 내 특정 데이터의 부모 데이터의 인덱스 반환.
부모 데이터가 존재하지 않으면 None을 반환.
"""
parent_index = child_index // 2
if parent_index >= 1:
return parent_index
return None
def _getChildIndex(self, parent_index: Index) \
-> (tuple[Index | None, Index | None]):
"""
힙 내의 특정 데이터의 두 (왼쪽, 오른쪽) 자식 데이터의 인덱스 반환.
자식 데이터가 존재하지 않을 경우의 반환값) \n
- 두 자식 데이터 모두 없는 경우: (None, None) \n
- 왼쪽 자식 데이터만 없는 경우: (None, Index) \n
- 오른쪽 자식 데이터만 없는 경우: (Index, None) \n
"""
lchild_index = parent_index * 2
rchild_index = parent_index * 2 + 1
if lchild_index > self.N:
lchild_index = None
if rchild_index > self.N:
rchild_index = None
return lchild_index, rchild_index
def _goUp(self, target_idx: Index) -> (None):
"""
enqueue를 통해 새 데이터 입력 시 힙 순위 특성에 맞게 재배치하기 위해
새 데이터를 우선순위에 따라 더 높은 층으로 이동시킨다.
매개변수
-------
target_idx: 새로 입력되어 힙 내에서 재배열이 필요한 데이터의 인덱스.
"""
parent_idx = self._getParentIndex(target_idx)
while parent_idx:
if self._less(parent_idx, target_idx):
self._swap(parent_idx, target_idx)
else:
# 이미 경로 내 정렬이 모두 끝났으므로 작업 종료.
break
def _goDown(self, target_idx: Index):
"""
dequeue 작업에 의해 맨 마지막에 있던 데이터가 최상위 층으로 이동한 경우,
힙 순서 특성을 맞추기 위해 해당 데이터의 위치를 필요한 만큼 힙 구조의
아래로 내려가게끔 하는 메서드.
매개변수
-------
target_idx: dequeue 작업에 의해 최상위 층으로 이동된 데이터의 인덱스.
"""
lchild_idx, rchild_idx = self._getChildIndex(target_idx)
while lchild_idx or rchild_idx:
if rchild_idx is None and self._less(target_idx, lchild_idx):
self._swap(target_idx, lchild_idx)
elif rchild_idx is None and not self._less(target_idx, lchild_idx):
break
if (self._less(target_idx, lchild_idx) or
self._less(target_idx, rchild_idx)):
if self._less(lchild_idx, rchild_idx):
self._swap(target_idx, rchild_idx)
target_idx = rchild_idx
else:
self._swap(target_idx, lchild_idx)
target_idx = lchild_idx
lchild_idx, rchild_idx = self._getChildIndex(target_idx)
else: break
def enqueue(self, v: Value, p: Priority) -> (None):
self.N += 1
#self.values[self.N], self.priorities[self.N] = v, p
self.values.append(v)
self.priorities.append(p)
self.location[v] = self.N
self._goUp(self.N)
def dequeue(self) -> (Value | None):
if self.isEmpty(): return
value_to_be_removed = self.values[1]
if self.N == 1:
self.N -= 1
return value_to_be_removed
self.values[1] = self.values.pop()
self.priorities[1] = self.priorities.pop()
self.location[self.values[1]] = 1
self.location.pop(value_to_be_removed)
self.N -= 1
self._goDown(1)
return value_to_be_removed
def decreasePriority(
self,
target_value: Value,
lower_priority: Priority
) -> (None):
"""
target_value 매개변수로 입력받은 값의 우선순위의 수치값을
lower_priority 매개변수로 입력받은 우선순위 수치값으로 낮춰서
해당 데이터의 우선순위를 키우는 메서드.
target_value의 우선순위 수치값은 lower_priority의 값보다 더
커야 한다.
"""
target_idx = self.location[target_value]
if self.priorities[target_idx] <= lower_priority:
error_msg = """
Error from decreasePriority() in class IndexedMinPQ.
target_value의 우선순위 값이 lower_priority의 값보다 더
작습니다.
"""
raise RuntimeError(error_msg)
self.priorities[target_idx] = lower_priority
self._goUp(target_idx)
이제 본격적으로 다익스트라 알고리즘을 구현하겠다. 다음의 코드는 예제 1-2의 클래스 안에 작성하였다.
def dijkstraAlgorithm(self) -> (None):
"""
weighted graph에서 가중치를 고려하여 source 노드로부터 특정 노드까지의
최단 거리와 그 경로를 구하는 함수. 해당 함수는 모든 가중치가 양수여야만
제대로 작동한다.
undirected graph에서도 잘 작동할 지 테스트 필요.
"""
# source node는 거리를 0으로 초기화하고, 나머지 노드들에 대해서는
# 모두 무한대(inf)로 지정한다.
dist_to: dict[Node, Distance] = {v:INF for v in self.graph.nodes()}
dist_to[self.src] = 0
impq = IndexedMinPQ() #2
impq.enqueue(self.src, dist_to[self.src])
for v in self.graph.nodes():
if v != self.src:
impq.enqueue(v, INF)
def relax(e) -> (None):
"""
source 노드에서 target 노드까지의 최단 거리를 탐색하는 함수.
"""
# edge (n, v)에서 노드 n, v와 가중치 weight를 추출.
n, v, weight = e[0], e[1], e[2]['weight'] #5
# 특정 노드로부터 n까지의 거리와 그 노드에서
# 노드 v로 향하는 edge weight 가중치 값을 더한 값이
# v로 직접 향하는 경로보다 더 짧으면 더 짧은 경로를 찾았다는 뜻.
# 따라서 해당 값을 새로 dist_to[v]에 갱신한다.
if dist_to[n] + weight < dist_to[v]: #6
dist_to[v] = dist_to[n] + weight #7
# Dijkstra 알고리즘을 통해 노드 v로 향하는 짧은 경로에 해당하는
# edge (n, v)를 기록.
edge_to[v] = e #8
# 노드 v의 우선순위 수치값을 새로 발견한 최단 거리값으로 낮춘다.
# 이를 통해 후에 while 문에서 최단 경로를 가지는 노드 추출이
# 가능해진다.
impq.decreasePriority(v, dist_to[v]) #9
# edge_to: 탐색 동안 찾은 v 노드로 향하는 edge를 기록.
edge_to: dict[Node, Edge] = {} #3
while not impq.isEmpty():
n = impq.dequeue() #4
# G.edges(data=True): edge의 가중치(weight) 추출을 위해
# data=True로 설정해줘야 함.
# n과 연결된 edge들을 반환.
for e in self.graph.edges(n, data=True):
relax(e)
self.dist_to = dist_to.copy()
self.edge_to = edge_to.copy()
다익스트라 알고리즘의 복잡도
해당 알고리즘의 시간복잡도를 따져보자. 이를 위해선 여러가지 요소들을 살펴보아야한다.
- 모든 노드들을 우선순위 큐에 삽입. 맨 처음에는 우선순위 수치값이 0인 source 노드가 삽입된다. 그 후, 모두 우선순위 값이 무한대로 똑같은 나머지 N-1개의 노드들이 삽입된다. 따라서 해당 연산의 시간복잡도는 O(N)이다.
- 우선순위 큐로부터 모든 노드들을 꺼내기 해당 알고리즘은 첫 노드부터 N번째 노드까지 차례대로 우선순위 큐 내의 노드를 하나씩 꺼내어 작업을 처리한다. 한 번 데이터를 꺼낼 때마다 우선순위 큐를 구성하는 이진 힙의 구조를 유지하기 위한 작업이 실행되는데, 해당 작업의 시간복잡도는 최악의 경우 O(log N)이다. 이러한 과정을 전체 노드에 대해 반복하기에, 결국 최악의 경우 해당 작업의 시간복잡도는 O(N log N)이다.
- 그래프 내 모든 간선에 접근하기 각각의 노드들로 향하는 거리값 계산을 위해서는 우선 인접한 간선들에 접근하여 해당 간선들의 가중치 값을 조사해야 한다. 만약 그래프 간선들이 인접 행렬로 저장되어 있는 경우, 모든 간선들을 조회(또는 추출)할 때의 시간복잡도는 \(O(N^2)\)이다. 반면, 그래프 간선들을 인접 리스트로 저장한 경우, 모든 간선들을 조회하는 데에 O(N+E)의 시간복잡도를 가진다.
- 간선들의 가중치, 즉 우선순위 값을 낮추기 위 코드의 relax() 함수는 모든 간선들에 대해 호출된다. 최악의 경우, 모든 간선들이 decreasePriority() 메서드의 호출에 의해 그 우선순위 값이 낮아진다. 즉, E번의 decreasePriority() 메서드 호출이 일어난다. 해당 메서드는 우선순위 값을 낮추면 힙의 순서 특성을 유지하기 위한 작업을 수행하게 된다. 이 작업의 시간복잡도는 O(log N)이다. 따라서 최종적으로 모든 노드들의 거리값이 새로 갱신되는 작업의 시간복잡도는 O(E log N)이 된다.
위 요소들을 모두 고려했을 때, 그래프의 구성을 인접리스트로 저장한 경우, 위에서 언급한 여러 시간복잡도들 중 가장 차수가 큰 항들은 O(N log N)과 O(E log N)이다. 따라서 인접 리스트 사용 시 다익스트라 알고리즘의 시간복잡도는 O((N+E) log N)이 된다. 만약 인접 행렬을 사용한다면 해당 알고리즘의 시간복잡도는 \(O(N^2)\)이 된다.
최단 경로 구성하기
다익스트라 알고리즘에서, 특정 노드로 향하는 간선을 저장하는 edge_to 변수를 사용하였다. 해당 변수를 이용하면, source 노드부터 target 노드까지의 최단 경로를 구성할 수 있다. 다음은 이를 수행하는 코드로, 예제 1-2의 클래스 안에 인스턴스 메서드로 작성되었다.
def reconstructShortestPath(self) -> (list[Node]):
"""
dijkstra 또는 bellman-ford 알고리즘을 통해 얻은 각 노드와
각 노드로 향하는 최단 거리 edge 정보를 담은 edge_to를 통해
source 노드로부터 target 노드까지의 최단 거리를
이루는 경로를 재구성하여 이를 반환하는 함수.
"""
if self.tar not in self.edge_to:
error_msg = f"""Error from function shortest_path().
target node {self.tar} is unreachable."""
raise ValueError(error_msg)
path: list[Node] = []
current_node = self.tar
while current_node != self.src:
path.append(current_node)
current_node = self.edge_to[current_node][0]
path.append(self.src)
path.reverse()
return path
또한, dist_to 변수를 통해 최단 경로의 거리만을 알 수도 있다. 다음의 코드도 해당 클래스에 이어서 작성한다.
def getShortestDistance(self) -> (Distance):
"""
source node로부터 target node로 가는 최단 거리를 반환.
"""
return self.dist_to[self.tar]
위 코드를 통해 그림 1에서 ‘a’ 노드에서 ‘c’ 노드로 향하는 최단 경로와 그 거리를 계산하면 다음의 결과를 얻는다.
['a', 'c']
3
음의 가중치가 존재할 경우 다익스트라 알고리즘이 제대로 작동하지 않는 이유
![그림 2-1. References [1]의 그림을 재구성함.](/images/2023-07-31/2023-07-31-algorithm-dijkstra-5.png)
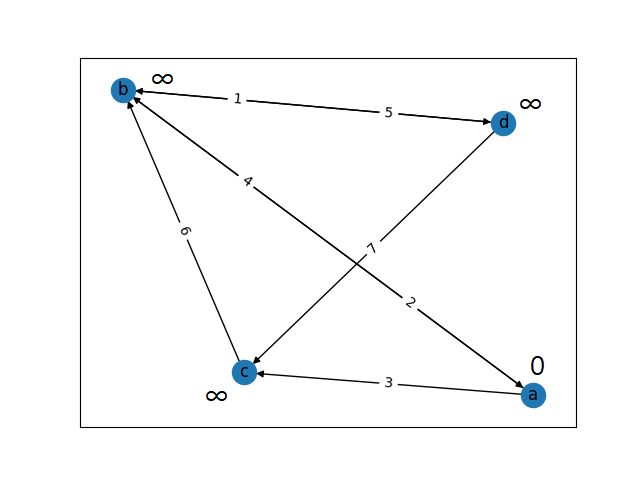
그림 2-1. References [1]의 그림을 재구성함.
![그림 2-2. References [1]의 그림을 재구성함.](/images/2023-07-31/2023-07-31-algorithm-dijkstra-6.png)
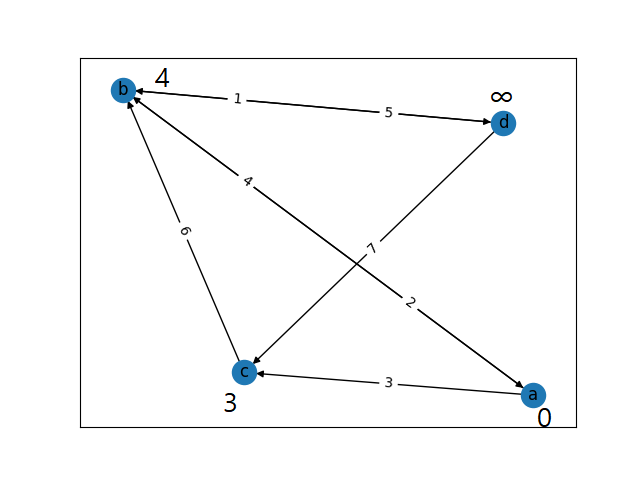
그림 2-2. References [1]의 그림을 재구성함.
![그림 2-3. References [1]의 그림을 재구성함.](/images/2023-07-31/2023-07-31-algorithm-dijkstra-7.png)
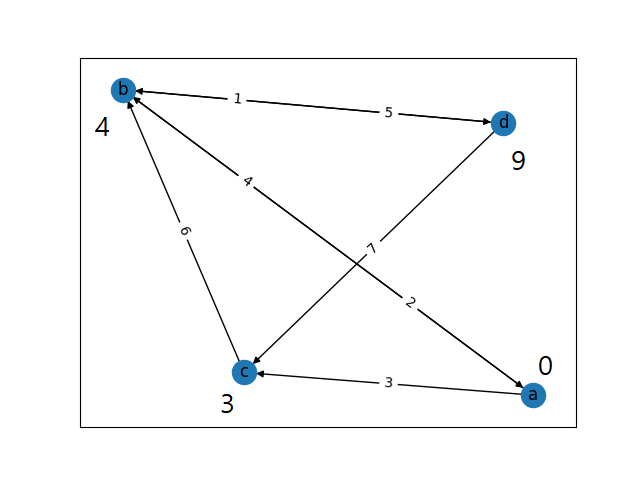
그림 2-3. References [1]의 그림을 재구성함.
위 그림들은 가중치 그래프에서 다익스트라 알고리즘을 이용하여 최단 경로를 탐색하는 과정을 묘사한 그림들이다. 앞서 다익스트라 알고리즘은 특정 v 노드에 대해 새로운 경로의 누적 거리가 기존 경로의 누적 거리보다 더 작을 경우 해당 누적 거리값으로 새롭게 갱신하고, 이 경우, 우선순위 내에 있는 v 노드의 우선순위 값도 해당 값으로 갱신하여 우선순위 값을 낮춘다고 하였다. 이러한 두 특성을 따라 위 그림 2의 각 노드에 대한 거리값들을 계산하면 결국엔 그림 2-3과 같은 결과가 나온다. 그림 2-3에서 우선순위 큐에 d가 가장 작은 우선순위 값을 가지므로 해당 노드가 큐에서 빠져나온다. 그런데 해당 노드의 out-degree = 0이므로 (즉, 앞으로 나아갈 간선이 없으므로) 아무런 작업도 하지 않는다. 이제 우선순위 큐에는 b만 남았다. 해당 노드를 큐에서 제거하고, 위에서 구현한 코드대로 동작하게끔 하면 에러가 발생할 것이다. 앞서 보인 코드에서 relax() 함수를 보면 간선 (n, v)가 있을 때 v가 우선순위 큐에 존재해야함을 전제로 하고 있다. 그런데 간선 (b, d)를 이루어야 할 노드 d가 이미 큐에 존재하지 않으므로 (b, d)에 대한 거리값 갱신을 할 수가 없게 된다.
이렇게 음의 가중치가 포함된 경우 문제가 발생하는 이유는 다익스트라 알고리즘이 인접한 간선의 가중치만을 보는 greedy 기반의 알고리즘이기 때문이다. 이전 문서의 A* 알고리즘 & Greedy Best-First Search 의 greedy BFS에서 알 수 있듯, greedy 기반 알고리즘은 한마디로 말해 “눈 앞의 이득만을 따지는” 알고리즘이다. 그래서 위 그림 2의 경우, 노드 a에서부터 인접 간선들의 가중치만을 고려하여 거리값을 계산하므로, 경로 a → c → d를 탐색할 때 걸리는 거리가 2이고, a → b를 탐색할 때 거리가 3이므로, 해당 알고리즘은 “a에서 b로 거치는 거리가 이미 3이니깐 안 봐도 a → c → d가 당연히 최단 경로겠지?”라고 판단하는 것이다. 즉, 다익스트라 알고리즘은 누적 거리를 계산할 때, 다른 노드로 나아가 검색할 수록, 누적 거리값은 동일하거나 증가하기만 할 것이라고 가정한다. 이는 곧 음수 가중치의 존재 자체를 상정하지 않는다는 뜻이기도 하다. 그렇기에 음수 가중치가 포함되어 있을 때 다익스트라 알고리즘이 제대로 작동하지 않는 것이다.
이를 해결하려면 Bellman-Ford 알고리즘을 이용해야 한다.
위에서 사용된 코드들의 풀버전 링크 : https://github.com/JeroCaller/ds-and-algo-in-python/blob/main/algorithms/graph/weighted_graph.py
Reference
[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)
[2] 파이썬 networkx weight 추가 & 그리기
[3] Weighted Graph — NetworkX 3.1 documentation
[4] Phind: AI Programming Assistant
[5] [NetworkX] 레이아웃으로 그래프 예쁘게 그리기 (nx layout)
[6] 최단 경로 문제: 다익스트라 알고리즘과 벨만-포드 알고리즘
This content is licensed under
CC BY-NC 4.0


댓글남기기