[알고리즘] 이진 트리 (Binary tree)
개요
이진 트리는 배열이나 연결 리스트와 같은 선형 자료구조와는 다른 비선형 자료구조이며, 이름에 “나무”가 있는 것처럼 한 노드가 왼쪽 또는 오른쪽 자식 노드 (또는 둘 다 가질 수 있다)를 가지고 그 자식 노드들이 또 다른 자식 노드들을 가지는 구조이다. 이진 트리는 재귀 자료구조 (recursive data structure)이다. 즉, 트리 구조 내에 똑같은 형태의 하위 트리 구조를 지니는 형태이다.
재귀 자료구조는 구조상의 결함을 갖지 않는다. 재귀 자료구조를 사용함으로써 발생하는 결함이나 에러 등은 모두 개발자의 프로그래밍적 실수이다. 예를 들어, 연결리스트를 구성하는 한 노드에 다음 노드를 가리키는 포인터 변수 next_pointer 가 자기 자신을 가리키도록 하면 에러가 발생하는데, 이것은 연결리스트라는 재귀 자료구조 자체의 결함이 아닌 개발자의 실수인 것이다.
이진 트리의 이점
이진 트리(이진 탐색 트리, Binary search tree라고도 불린다)는 데이터의 삽입, 검색, 삭제 연산을 좀 더 효율적으로 수행할 수 있는 재귀적 자료구조라 볼 수 있다. 일단 이진 트리의 데이터의 검색, 삽입, 삭제 연산의 (최악의 경우) 시간복잡도는 O(log N)으로 알려져 있다. 이는 배열을 이용하는 것보다 더 효율적인 복잡도임을 알 수 있다. 이 외에도 배열에 비해 이진 트리가 가진 장점은 다음과 같다.
- 배열에서는 새로운 데이터를 추가하려면 새로운 데이터가 추가되었을 때의 총 데이터 수에 맞는 (즉 N+1개의) 새로운 배열을 생성한 후, 기존 배열의 데이터들을 모두 해당 배열에 복사해야한다. (이후 기존 배열에 대한 메모리는 할당 해제된다) 그리고 새로운 데이터가 삽입될 자리가 맨 오른쪽 끝이 아닌 중간인 경우, 새로운 데이터가 삽입될 위치부터 그 오른쪽의 모든 데이터들이 한 칸씩 오른쪽으로 옮겨져야 한다. 반면, 이진트리는 새로운 데이터를 담는 새로운 노드를 형성한 뒤 그저 부모 노드가 해당 노드를 가리키게 하면 될 뿐이다.
- 배열에서 어떤 값을 삭제하고자 한다면, 삭제 후 그 오른쪽에 위치한 모든 데이터들을 왼쪽으로 한 칸씩 옮겨야 한다. 이 한 칸씩 옮기는 작업은 최악의 경우 O(N)의 시간복잡도를 가진다. 하지만 이진 트리의 경우 삭제 작업의 시간복잡도는 O(log N)으로 더 효율적이다.
파이썬 내장 자료형인 list는 배열과 달리 동적으로 그 크기를 조절할 수 있다. 하지만 삽입, 삭제, 검색의 최악의 경우 시간복잡도는 O(N)으로, 이진 트리에 비해 덜 효율적이다.
이진 트리의 개념 및 구조, 그리고 데이터 삽입
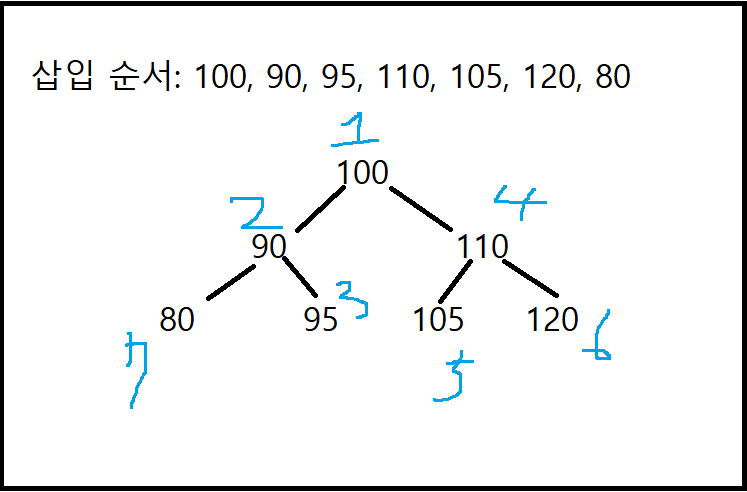
그림 1-1. 이진 트리의 구조 예시.
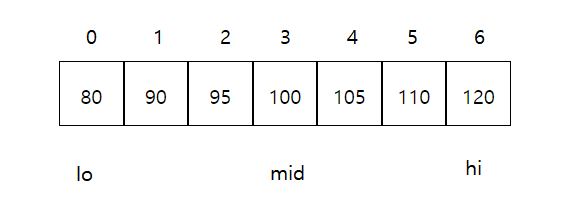
그림 1-2. 이진 트리를 이진 배열로 나타낸 그림.
이진 트리는 그림 1-1과 같은 구조를 가진다. 이진 트리를 1차원의 배열로 재구성하면 그림 1-2와 같이 이진 배열 탐색으로 환원된다.
이진 트리에서의 가장 위에 있는 노드를 root(뿌리)라고 한다. 그리고 이진 트리를 구성하는 각 노드들은 각각 왼쪽 자식 노드와 오른쪽 자식 노드를 가질 수 있는데, 왼쪽, 오른쪽 자식 노드 모두 가지지 않는 노드를 leaf(잎) 노드라 부른다.
그림 1을 보면 알 수 있듯, 어떤 노드의 자식 노드는 하위 이진 트리의 root 노드가 되기도 한다. 어떤 노드를 root 노드로 하는 하위 이진 트리의 범위는 해당 root노드와 직간접적으로 아래에서 연결되어 있는 모든 자식 노드들을 포함한다. (해당 root 노드의 상위 노드들은 해당 하위 트리 범위에 들지 않는다) 이 논리에 따르면 이진 트리 내의 하위 트리들은 모두 왼쪽 하위 트리와 오른쪽 하위 트리로 구분할 수 있다.
또한 숫자 값을 가지는 노드들이 이진 트리를 구성할 때에도 규칙이 있다. 첫 째는 숫자 값 n을 가지는 노드의 왼쪽 하위 트리를 구성하는 모든 자식 노드들은 해당 노드 n보다 더 작거나 같은 값만을 가진다. 둘 째는, 숫자 값 n을 가지는 부모 노드의 오른쪽 하위 트리를 구성하는 모든 자식 노드들의 값은 모두 부모 노드의 값 n보다 같거나 큰 값만을 가진다. 즉, 정리하자면 왼쪽 자식 노드의 값 < 부모 노드의 값 < 오른쪽 자식 노드의 값이라는 조건을 만족시켜야 한다. 이러한 조건을 지키면서 이진 트리에 새로운 값들을 차례대로 삽입하는 과정은 다음과 같다.

그림 2. 이진 트리 내 데이터 삽입 예시.
그림 2를 예로 들 때, 삽입 순서와 그림 2의 위에 언급된 순서대로라면 삽입 과정은 다음과 같이 이루어진다.
- 이진 트리 내에 아무런 노드가 없으므로 100을 값으로 가지는 새로운 노드를 생성하여 이를 이진 트리내에 삽입한다. 해당 노드는 root 노드가 된다.
- 두 번째 데이터인 90을 값으로 가지는 새로운 노드를 형성한 뒤, root 노드의 값 100과 대소 비교한다. 90 < 100 이므로 90을 가지는 노드는 100을 가지는 노드의 왼쪽 하위 트리 내에 삽입되어야 한다. 그런데 해당 하위 트리는 존재하지 않는 상태이므로 100을 가지는 노드는 직접 90을 가지는 노드와 연결된다. 이제 90을 가지는 노드는 100을 가지는 노드의 왼쪽 하위 트리의 root 노드가 된다.
- 세 번째 데이터 95를 값으로 담을 새로운 노드를 형성한다. 그 후 최상위 root 노드부터 그 값을 대소 비교한다. 95 < 100이므로 100을 가지는 노드의 왼쪽 하위 트리로 빠진다. 이 때 왼쪽 하위 트리에는 90을 가지는 하위 노드가 존재하므로 또 한 번 이 노드의 값 90과 대소 비교를 한다. 95 > 90이므로 95를 가지는 노드는 90을 가지는 노드의 오른쪽 하위 트리로 빠진다. 이 때, 해당 하위 트리가 존재하지 않으므로 90을 가지는 노드는 95를 가지는 노드와 직접적으로 연결되어 95를 가지는 노드는 90을 가지는 노드의 오른쪽 자식 노드가 된다. 95를 가지는 노드는 90을 가지는 노드의 오른쪽 하위 트리의 root 노드가 되는 셈이다.
- 네 번째 데이터 110을 가지는 새로운 노드가 형성되어 이진 트리에 삽입된다. 이 때 최상위 root 노드인 100부터 그 값끼리 대소비교를 한다. 110 > 100이므로 110 노드는 100 노드의 오른쪽으로 보내진다. 이 때 해당 자리에는 아무것도 없으므로 100을 가지는 노드와 직접적으로 연결된다.
- 이렇게 새로운 데이터가 삽입될 때마다 새로운 노드가 형성되어 해당 데이터를 값(value)으로 가지며, 이진 트리의 최상위 노드의 값부터 대소비교하여 왼쪽 또는 오른쪽 하위 트리로 이동하고 또 값을 비교하고 내려가는 형태를 띤다. 이러한 과정은 새로운 노드가 leaf 노드로 안착될 때까지 반복한다.
이를 파이썬 코드로 구현하면 다음과 같다. 먼저 노드 객체를 정의하는 코드이다.
# type alias
BNode_ = object # BNode 객체
NodeValue = int
class BNode():
"""
이진 트리 (binary tree)를 구성하는 노드를 구현하는 클래스.
"""
def __init__(self, value_: NodeValue, depth: int = 0):
"""
매개변수) \n
value: 노드에 저장될 값. \n
depth: 이진 트리 내에서 해당 노드의 깊이.
root는 깊이를 0이라 가정.
자식 쪽으로 한 칸씩 내려갈수록 깊이가 1씩 증가.
속성) \n
self.__left: 노드의 왼쪽 자식 노드. \n
self.__right: 노드의 오른쪽 자식 노드. \n
self.__value: 노드의 값. \n
self._node_depth: 해당 노드의 이진 트리 내 깊이. \n
self._node_number: 해당 노드의 숫자. BF를 구하는 용도. \n
"""
self.__value: NodeValue = value_
self.__left: BNode | None = None
self.__right: BNode | None = None
self._node_depth: int = depth
def __lt__(self, other: BNode_): return self.depth < other.depth
def __repr__(self):
basic_info = f"Node object. its value: {self.value}, " + \
f"its depth in BT: {self.depth}, height: {self.height}"
lc = self.leftChild.value if self.leftChild else None
rc = self.rightChild.value if self.rightChild else None
additional_info = f" lc.value: {lc}, rc.value: {rc}"
return basic_info + additional_info
@property
def value(self) -> NodeValue: return self.__value
@value.setter
def value(self, new_value: NodeValue) -> None: self.__value = new_value
@property
def leftChild(self) -> BNode_ | None: return self.__left
@leftChild.setter
def leftChild(self, new_left: BNode_) -> None: self.__left = new_left
@property
def rightChild(self) -> BNode_ | None: return self.__right
@rightChild.setter
def rightChild(self, new_right: BNode_) -> None: self.__right = new_right
@property
def depth(self) -> int: return self._node_depth
@depth.setter
def depth(self, new_depth: int) -> None: self._node_depth = new_depth
그리고 이진 트리를 구현하는 클래스 BinaryTree를 정의한 후, 그 안에 데이터를 삽입하는 기능을 가진 메서드들을 다음과 같이 구현하였다.
class BinaryTree():
"""
왼쪽 자식 노드의 값 < 부모 노드의 값 < 오른쪽 노드의 값.
"""
def __init__(self):
self._root: BNode | None = None
self._node_depth = 0
self._num_node = 0 # 이진 트리 내 총 노드 개수.
def insert(self, new_value: NodeValue) -> None:
self._node_depth = 0
self._root = self._insert(self._root, new_value)
self._num_node += 1
def _insert(
self,
node: BNode | None,
value: NodeValue
) -> BNode:
"""
self.insert() 메서드를 돕는 서브 메서드.
반환값은 node 매개변수로 대입된 루트 노드.
"""
if node is None: return BNode(value, self._node_depth)
self._node_depth += 1
if value <= node.value:
node.leftChild = self._insert(node.leftChild, value)
else:
node.rightChild = self._insert(node.rightChild, value)
return node
예제 1-2의 _insert() 메서드 구조를 보면 자기 자신을 호출하는 재귀 함수이다. 이는 이진 트리가 재귀적 자료구조를 띤다는 점에서 재귀 함수를 이용한 것이다.
한 편, 그림 2에서의 데이터들을 오름차순으로 이진 트리에 삽입하면 그림 2와 전혀 다른 구조가 나타난다.
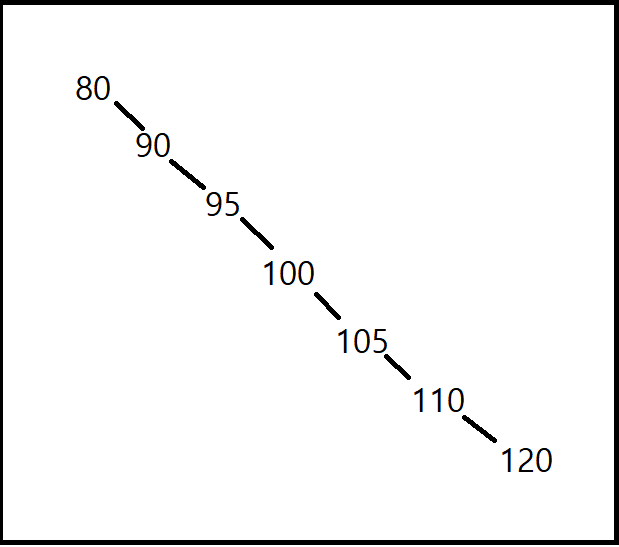
그림 3. 이진 트리 내에 데이터들이 삽입되는 최악의 경우. 값들을 오름차순으로 대입할 때 발생한다.
데이터들을 오름차순(또는 내림차순)으로 이진 트리에 삽입하면 그림 3과 같은 형태를 지니게 된다. 이는 사실상 연결 리스트와 같다. 이 경우 데이터 삽입의 시간복잡도가 O(N)이 되어 이진 트리의 장점이 사라진다. 이를 해결하는 방법은 후에 기술할 것이다.
이진 트리에서 데이터 검색하기
앞서 데이터 삽입을 위해 삽입 메서드는 leaf 노드를 발견할 때까지 재귀적으로 탐색한 후 새로운 데이터를 삽입하는 구조를 가졌다. 이진 트리 내 데이터 검색도 마찬가지로 재귀적으로 탐색하여 원하는 데이터가 이진 트리에 있는지 검색할 수 있다.
다음은 이진 트리 내에 특정 값이 있는지를 True 또는 False로 반환하여 알려주는 메서드 구현 코드 예이다.
class BinaryTree():
# (중략)
def __contains__(self, target_value: NodeValue) -> bool:
"""
이진 트리에 특정 값이 있는지 조사. 있는지 없는지만 알려준다.
사용법: target_value in BinaryTree 객체.
반환값은 반드시 bool이어야 함.
"""
node = self._root
while node:
if target_value == node.value: return True
if target_value < node.value: node = node.leftChild
else: node = node.rightChild
return False
만약 특정 값을 가지는 노드 자체를 반환받고자 한다면 다음과 같이 구현할 수도 있다.
class BinaryTree():
# (중략)
def search(self, target_value: NodeValue) -> BNode | None:
"""
찾고자 하는 값과 일치하는 노드를 반환.
"""
return self._search(self._root, target_value)
def _search(
self,
node: BNode,
target_value: NodeValue
) -> BNode | None:
"""
self.search() 메서드를 돕는 서브 메서드.
"""
if node is None: return None
if node.value == target_value: return node
elif node.value > target_value:
node = self._search(node.leftChild, target_value)
else:
node = self._search(node.rightChild, target_value)
return node
이진 트리 내에서 데이터 삭제하기
이진 트리 내에서 특정 데이터를 삭제하는 것 자체는 앞서 살펴본 데이터 검색처럼 해당 데이터를 검색한 후 해당 데이터를 지우기만 하면 된다. 그러나 이러면 이진 트리의 구조를 더 이상 유지할 수 없다. 따라서 특정 데이터를 삭제한 뒤에도 이진 트리의 구조를 효율적으로 유지할 어떤 방법이 필요하다. 사실 이를 위한 두 가지 방법이 있다.
- 삭제될 노드의 왼쪽 하위 트리 중에서 최대값을 찾아 삭제될 노드 자리를 채운다.
- 삭제될 노드의 오른쪽 하위 트리 중에서 최소값을 찾아 삭제될 노드 자리를 채운다.
각각의 두 방법으로 최소값 또는 최대값을 찾고자 할 때 최소값 또는 최대값을 가지는 노드의 특징을 통해 찾을 수 있다.
- 삭제될 노드의 왼쪽 하위 트리 중에서 최대값을 찾고자할 때, 최대값을 가지는 노드는 오른쪽 자식 노드를 가지지 않는다.
- 삭제될 노드의 오른쪽 하위 트리 중에서 최소값을 찾고자할 때 최소값을 가지는 노드는 왼쪽 자식 노드를 가지지 않는다.
지금부터는 2번: 오른쪽 하위 트리 중 최소값을 가지는 노드를 찾아 삭제될 노드 자리를 채우는 방법을 중심으로 설명하겠다.
최소값을 찾았다면, 해당 노드를 삭제하여 빈 자리에 채우면 된다. 그러면 이 때 최소값을 가지는 노드의 자리가 비게 되는데, 만약 해당 노드가 원래 오른쪽 하위 트리를 가지고 있었다면 해당 하위 트리의 root 노드로 대신하면 된다. (즉, 최소값 노드의 오른쪽 하위 트리가 한 칸씩 위로 올라온다고 생각하면 된다)
다음은 삭제하고자 하는 특정 값이 주어지면 그에 해당하는 노드를 이진 트리에서 제거하고, 빈 자리를 앞서 언급한 방식으로 채우도록 하는 코드이다.
class BinaryTree():
# (중략)
def remove(self, target_value: NodeValue) -> None:
self._root = self._remove(self._root, target_value)
def _remove(
self,
node: BNode | None,
target_value: NodeValue
) -> BNode | None:
"""
self.remove() 메서드를 돕는 서브 메서드.
반환값은 매개변수 node. 단, 이 메서드를 실행하고 나면
구조가 바뀐 하위 트리를 가지게 될 것이다.
"""
if node is None: return None
if target_value < node.value:
node.leftChild = self._remove(node.leftChild, target_value)
elif target_value > node.value:
node.rightChild = self._remove(node.rightChild, target_value)
else:
if node.leftChild is None:
self._num_node -= 1
if node.rightChild: node.rightChild.depth -= 1
return node.rightChild
if node.rightChild is None:
self._num_node -= 1
if node.leftChild: node.leftChild.depth -= 1
return node.leftChild
# 아래 코드는 삭제하고자 하는 노드가 두 자식 노드를
# 모두 가지고 있을 경우를 처리하는 코드임.
node_to_be_removed: BNode = node
depth_of_original = node.depth
# 삭제되어 사라질 노드 자리를 대체하기 위해
# 대체할 노드를 삭제할 노드의 오른쪽 하위 트리의
# 최소값을 가지는 노드로 가져와 대체한다.
# 이를 위해 우선 삭제할 노드의 오른쪽 노드를 먼저
# 가리켜야 한다.
node = node.rightChild
# 최소값을 가지는 노드는 왼쪽 자식 노드를 가지지 않는 노드이다.
# 해당 노드를 탐색한다.
while node.leftChild: node = node.leftChild
node.rightChild = self._removeMin(node_to_be_removed.rightChild)
# 삭제될 노드의 빈자리를 채우는 최소값 노드의 왼쪽 자식 노드는
# 삭제될 노드의 왼쪽 자식 노드를 가리키도록 한다.
node.leftChild = node_to_be_removed.leftChild
node.depth = depth_of_original
self._num_node -= 1
return node
def _removeMin(self, node: BNode) -> BNode | None:
"""
self._remove() 메서드를 돕는 서브 메서드.
최소값을 가지는 노드가 삭제될 노드 자리로 갈 때,
최소값을 가지는 노드의 빈자리를
최소값 노드의 하위 오른쪽 자식 노드로 대체.
반환값은 구조 조정을 마친 루트 노드.
"""
if node.leftChild is None: return node.rightChild
node.leftChild = self._removeMin(node.leftChild)
node.leftChild.depth -= 1
return node
_remove()와 _removeMin() 메서드 모두 반환값은 구조가 재조정된 하위 트리를 가지는 root 노드이다.
트리 순회 (Traversing a Binary tree)
이진 트리 내 모든 노드들을 순회하여 이 모든 노드들을 반환하고자 한다. 앞서 말했듯 이진 트리는 재귀적인 구조를 띄기에 재귀 호출을 이용하는 것이 좋다. 다음은 Generator로 구성하여 이진 트리 내 모든 값들을 값들의 오름차순으로 반복(iterate)하는 코드이다.
class BinaryTree():
"""
왼쪽 자식 노드의 값 < 부모 노드의 값 < 오른쪽 노드의 값.
"""
def __init__(self):
# (중략)
self._ascending_with_node: bool = False
def ascendingOrderWithNode(self, mode_set=False) -> None:
"""
오름차순으로 노드 반환 시 노드 자체를 반환할 것인지,
노드의 값들만을 반환할 것인지를 설정하는 메서드.
True시 노드 자체를 반환. False시 노드의 값만 반환.
"""
self._ascending_with_node = mode_set
def __iter__(self) \
-> Generator[BNode, BNode, BNode] \
| Generator[NodeValue, NodeValue, NodeValue] | None:
"""
이진 트리 내 모든 노드들을 노드 값들의 오름차순으로
반환하는 이터레이터.
"""
if self._ascending_with_node:
for node in self._ascendingOrder(self._root):
yield node
else:
for value in self._ascendingOrder(self._root):
yield value
def _ascendingOrder(
self,
node: BNode
) \
-> Generator[BNode, BNode, BNode] \
| Generator[NodeValue, NodeValue, NodeValue] | None:
"""
왼쪽 자식 노드 값 < 부모 노드 값 < 오른쪽 자식 노드 값이란
사실을 이용하여 오름차순으로 숫자들을 반환한다.
"""
if node is None: return
if self._ascending_with_node:
for nod in self._ascendingOrder(node.leftChild):
yield nod
yield node
for nod in self._ascendingOrder(node.rightChild):
yield nod
else:
for value in self._ascendingOrder(node.leftChild):
yield value
yield node.value
for value in self._ascendingOrder(node.rightChild):
yield value
순회 방식
이진 트리를 순회할 때 부모 노드와 왼쪽 하위 트리, 오른쪽 하위 트리 중 어느 것을 어느 순서대로 탐색하느냐에 따른 방식이 구분되어 있다.
- 전위 순회 (pre-order): 부모 노드를 먼저 탐색한 후, 부모 노드의 왼쪽 하위 트리를 탐색, 그 후 오른쪽 하위 트리를 탐색하는 방식. 즉, 부모 노드 → 왼쪽 → 오른쪽 순이다.
- 중위 순회 (in-order): 왼쪽 하위 트리 → 부모 노드 → 오른쪽 하위 트리 순으로 탐색한다. (예제 4-1이 중위 순회 방식을 채택한 예이다)
- 후위 순회 (post-order): 왼쪽 하위 트리 → 오른쪽 하위 트리 → 부모 노드 순으로 탐색하는 방법.
- 레벨 순회 (level-order) : 깊이가 같은 노드, 즉 레벨이 같은 노드들을 탐색하는 방식. 너비 우선 순회(Breadth-first traversal)라고도 불린다고 한다.
이진 탐색 트리의 성능
앞서 살펴본 이진 트리 내의 데이터 삽입, 검색, 삭제 연산들은 모두 leaf 노드에서 root 노드까지의 높이(height)에 의존한다.
이진 트리는 크게 각 k층의 노드의 개수가 \(2^k\)으로 꽉 차 있는(즉, leaf 노드를 제외한 모든 노드들이 왼쪽 자식 노드와 오른쪽 자식 노드를 모두 가지는 구조) 완전 이진 트리 (complete binary tree)와 각 하위 트리의 높이가 제각기 다른 불균형 트리 (unbalanced tree)로 구분지을 수 있는데, 최선의 경우는 완전 이진 트리로, 데이터의 삽입, 검색, 삭제 모두 최선의 경우 시간복잡도는 O(log N)이다. 그러나 최악의 경우는 그림 3처럼 모든 데이터가 오름차순 또는 내림차순으로 삽입되어 직선을 이루는 경우로, 최악의 경우 시간복잡도는 O(N)이 된다.
일반적으로는 불균형 트리를 이루는 경우가 많다. 그래서 이 경우의 데이터 삽입, 검색, 삭제의 시간복잡도는 보통 O(h)이다. 여기서 h는 앞서 말했듯 특정 leaf 노드에서 root 노드까지의 높이를 의미한다.
그러면 데이터 삽입, 삭제, 검색의 시간복잡도가 최악의 경우라도 O(log N)이 되도록 하여 좀 더 효율적인 삽입, 삭제, 검색을 하도록 하는 방법은 없을까? 다음 장에서는 완전 이진 트리까지는 아니더라도 그에 준하도록 균형을 맞추는 이진 트리에 대해서 살펴보겠다.
자가 균형 이진 트리 (Self-balancing binary tree)
자가 균형 이진 트리 중의 하나로 AVL tree라는 방법이 있다. 이는 이진 트리 내에 높이의 차이가 커져서 불균형한 상태를 자동으로 감지하여 이를 자동으로 균형을 맞추는 이진 트리이다.
이진 트리 내에서 왼쪽 하위 트리의 높이와 오른쪽 하위 트리의 높이가 다른 것을 자동으로 감지하는 방법은 다음과 같다. 먼저 노드 객체는 각자 자신의 높이 height를 기록하는 변수가 있어야 한다. 그 후, 데이터가 삽입, 삭제될 때마다 왼쪽 하위 트리의 높이에서 오른쪽 하위 트리의 높이를 뺀다. 만약 왼쪽으로 기울어져 있다면, 즉 왼쪽 하위 트리의 높이가 상대적으로 더 크다면 그 결과는 양수가 나올 것이고, 오른쪽으로 기울어져있다면 음수가 나올 것이다. 만약 어느 쪽으로도 기울어지지 않았다면, 즉, 왼쪽 하위 트리의 높이와 오른쪽 하위 트리의 높이가 같다면 0이 나올 것이다. 참고로, 왼쪽 하위 트리의 높이에서 오른쪽 하위 트리의 높이를 뺀 값을 Balance Factor(BF)라고 부른다. BF는 모든 노드에서 계산 가능하다.
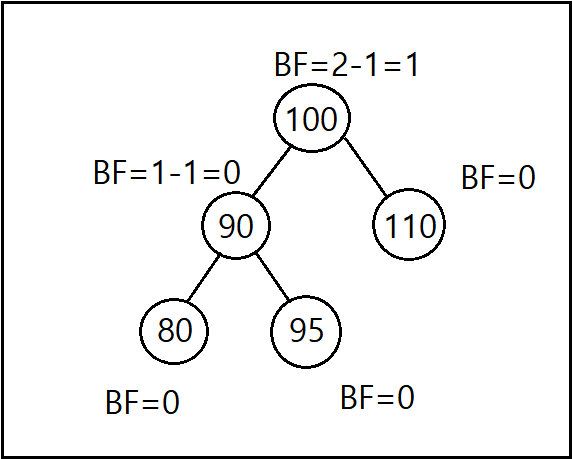
그림 4. 각 노드의 BF와 AVL Tree 예시.
AVL Tree는 모든 노드들의 BF가 -1, 0, 1중 하나가 되도록 자가 균형을 이루는 이진 트리이다. 만약 이 범위를 벗어난다면 AVL Tree는 이를 감지하고 자동으로 균형을 이루도록 한다. (균형을 이루는 방법에 대해서는 다음에 기술)
각 노드의 높이값을 저장하는 변수와 데이터가 삽입, 삭제될 때마다 노드의 높이를 다시 계산해주는 메서드, 그리고 해당 노드의 BF를 구하는 메서드를 노드 객체에 구현하였다.
class BNode():
"""
이진 트리 (binary tree)를 구성하는 노드를 구현하는 클래스.
"""
def __init__(self, value_: NodeValue, depth: int = 0):
"""
매개변수) \n
value: 노드에 저장될 값. \n
depth: 이진 트리 내에서 해당 노드의 깊이.
root는 깊이를 0이라 가정.
자식 쪽으로 한 칸씩 내려갈수록 깊이가 1씩 증가.
속성) \n
self.__left: 노드의 왼쪽 자식 노드. \n
self.__right: 노드의 오른쪽 자식 노드. \n
self.__value: 노드의 값. \n
self._node_depth: 해당 노드의 이진 트리 내 깊이. \n
self._node_number: 해당 노드의 숫자. BF를 구하는 용도. \n
"""
self.__value: NodeValue = value_
self.__left: BNode | None = None
self.__right: BNode | None = None
self._node_depth: int = depth
self.__node_height: int = 1 # 1 이상이어야 함.
# (중략)
def calculateNodeHeight(self) -> None:
"""
해당 노드의 높이를 계산하는 메서드.
노드 높이는 Balance factor 계산에 쓰인다.
"""
left_num = self.leftChild.height if self.leftChild else 0
right_num = self.rightChild.height if self.rightChild else 0
self.height = max(left_num, right_num) + 1
def BalanceFactor(self) -> int:
"""
루트 노드의 각각 왼쪽과 오른쪽 하위 트리의 깊이 차를 구하는 메서드.
BF = 왼쪽 하위 트리의 깊이 - 오른쪽 하위 트리의 깊이.
BF > 0 -> 왼쪽 하위 트리가 더 깊음(왼쪽으로 쏠림).
BF < 0 -> 오른쪽 하위 트리가 더 깊음(오른쪽으로 쏠림).
"""
left_num = self.leftChild.height if self.leftChild else 0
right_num = self.rightChild.height if self.rightChild else 0
return left_num - right_num
@property
def height(self) -> int: return self.__node_height
@height.setter
def height(self, new_height: int) -> None: self.__node_height = new_height
어떤 곳에서는 leaf 노드의 높이를 0으로 시작하는 곳이 있지만, 여기서는 “BF는 결국 왼쪽 하위 트리 중 가장 높이가 큰 노드들의 개수를 세고, 오른쪽 하위 트리에 대해서도 똑같이 노드들의 개수를 세어 이 둘을 빼는 것”이라는 생각에 leaf 노드의 높이를 1로 설정하였다. (보통 무언가를 셀 때는 0부터 세지 않고 1부터 세니깐)
다음은 앞서 구현한 BinaryTree 클래스를 상속하는 AVLTree라는 클래스를 따로 만들고, 그 안에 _insert() 메서드의 코드를 일부 바꾼 예제이다.
class AVLTree(BinaryTree):
"""
자가 균형 이진 트리 중 하나. 왼쪽 하위 트리와 오른쪽 하위 트리의 불균형을
스스로 탐지하고 이를 스스로 고쳐 균형을 유지한다.
"""
# (중략)
def __init__(self):
super().__init__()
def _insert(
self,
node: BNode | None,
value: NodeValue
) -> BNode:
"""
self.insert() 메서드를 돕는 서브 메서드.
반환값은 node 매개변수로 대입된 루트 노드.
"""
if node is None: return BNode(value, self._node_depth)
self._node_depth += 1
if value <= node.value:
node.leftChild = self._insert(node.leftChild, value)
else:
node.rightChild = self._insert(node.rightChild, value)
node.calculateNodeHeight() #1
return node
예제 1-2와 비교해봤을 때 달라진 점은 #1 부분에 노드의 높이를 계산해주는 메서드가 추가되었다는 점이다. 해당 코드의 추가로 인해, 데이터가 삽입될 때마다 새로운 데이터가 삽입되는 경로에 놓인 모든 노드들의 높이가 다시 계산되어 업데이트된다. (새로운 데이터가 삽입되는 경로에 놓여있지 않은 다른 노드들에 대해서는 변경사항이 없기에 높이를 다시 계산할 필요가 없다)
_remove() 메서드와 _removeMin() 메서드에 대해 노드의 높이를 계산하는 메서드를 삽입하는 부분은 앞으로 설명할 불균형 트리의 균형을 자동으로 맞추는 방법을 설명할 때 같이 보일 예정이다.
위 과정을 통해 데이터가 삽입, 삭제될 때마다 각 노드들의 높이가 다시 계산되고, BF를 계산하여 실시간으로 이진 트리의 균형이 깨졌는지를 감지한다. 이번에는 만약 균형이 깨졌다면 이를 어떻게 해결하여 균형을 맞출 지에 대해 살펴보겟다.
노드 회전 (node rotation)
불균형한 트리의 균형을 맞추는 방법으로 노드를 회전시키는 방법이 있다. 다음은 모든 가능한 불균형한 경우에 대해 균형을 맞추기 위한 노드 회전법을 묘사한 그림이다.
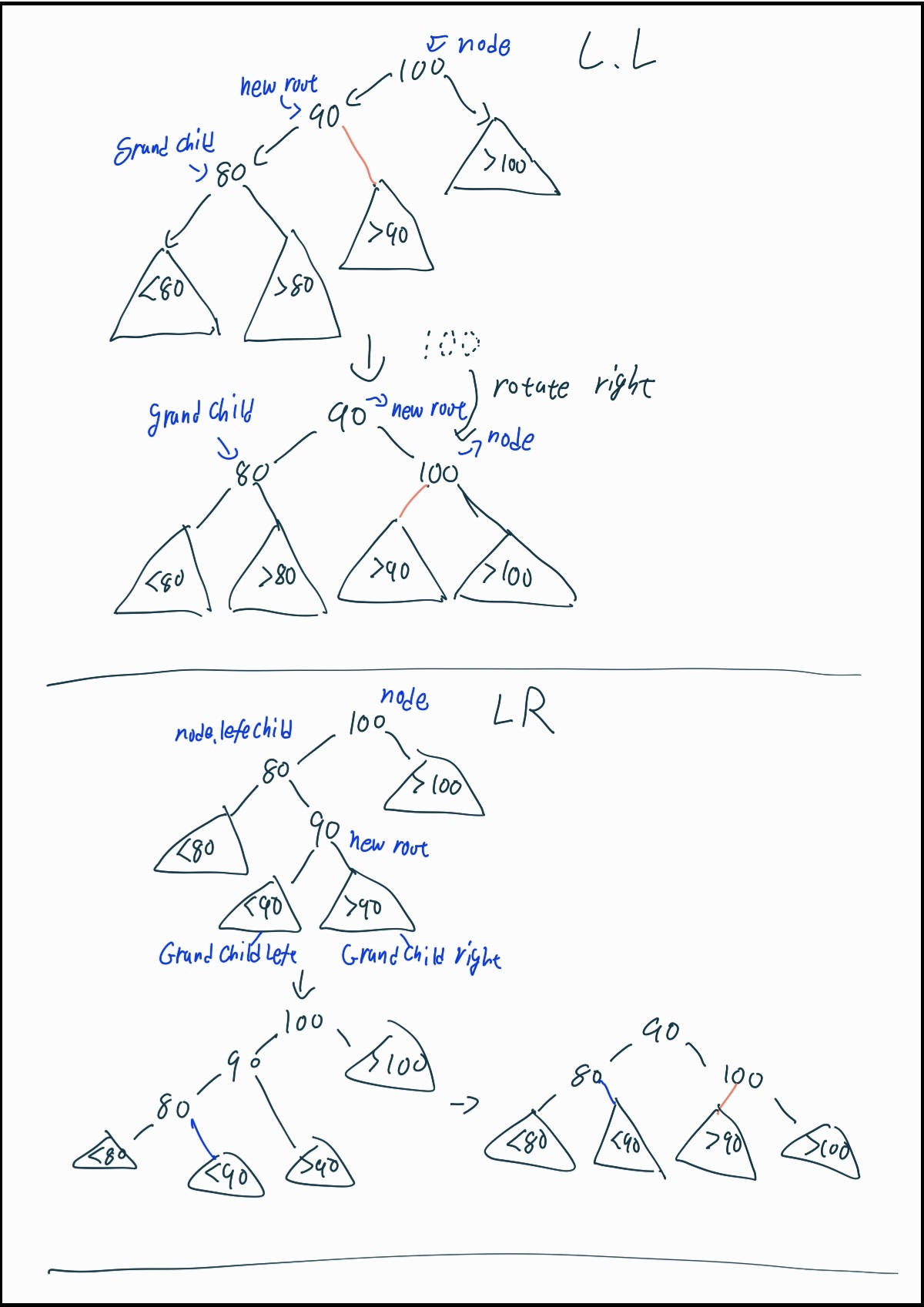
그림 5-1. 불균형한 노드가 각각 Left-Left(LL), Left-Right(LR)일 때 이를 해결하는 방법. 마치 노드를 회전시키는 것 같아서 노드 회전(node rotation)이라고 불리기도 한다. 참고로 삼각형으로 표시한 곳은 하위 트리를 묘사한 것이다.
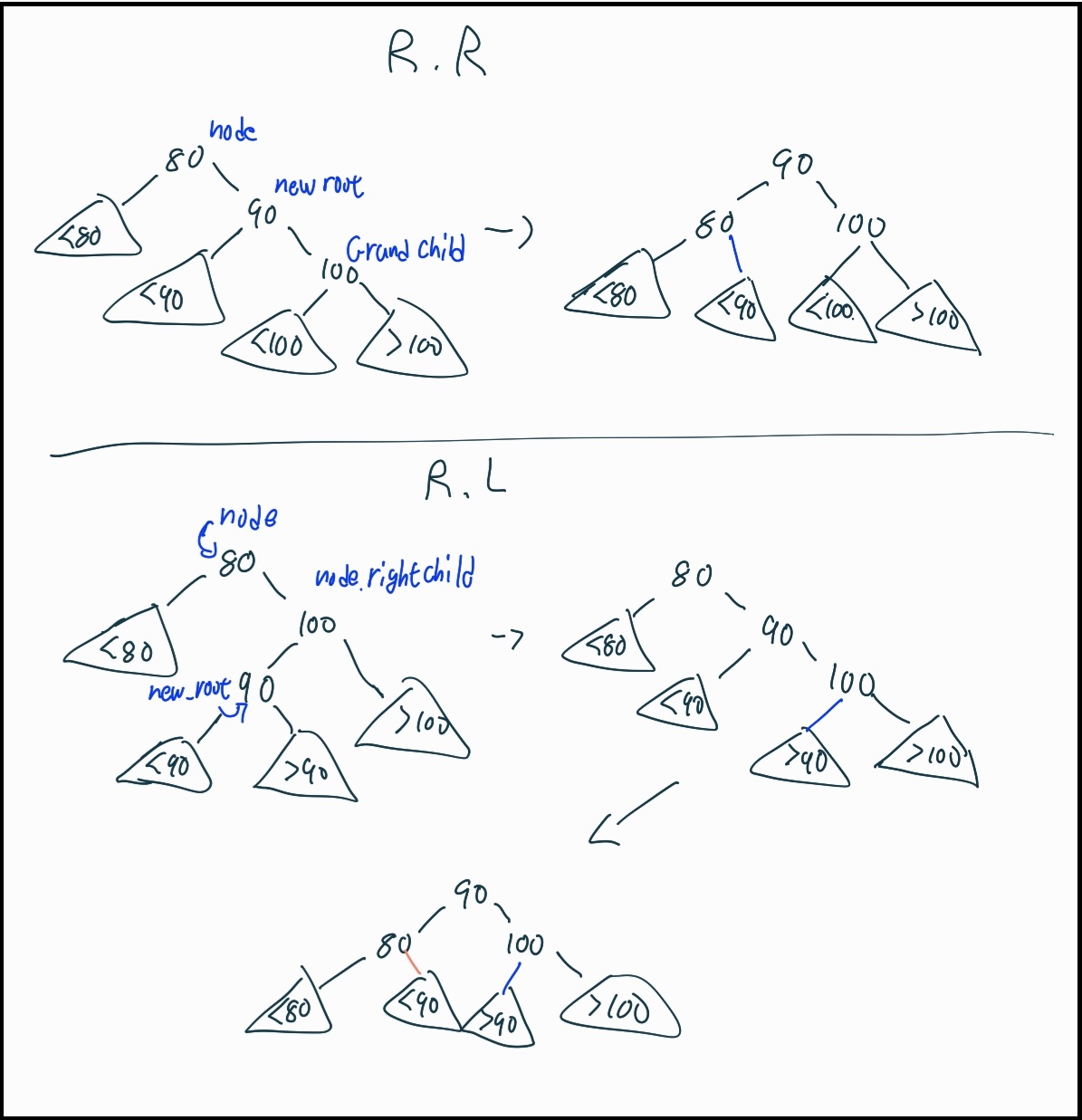
그림 5-2. 불균형한 노드의 구조가 각각 Right-Right(RR), Right-Left(RL)일 때 이를 해결하는 방법.
불균형한 경우로 각각 LL, LR, RR, RL의 경우가 있는데, 각각 다음을 말한다.
- LL(Left-Left): root 노드를 중심으로 왼쪽 자식 노드 → 왼쪽 손주 노드 구조로 불균형해진 경우. 위 그림 5-1의 LL이라고 표기한 그림이 예시이다.
- LR(Left-RIght): root 노드를 중심으로 왼쪽 자식 노드 → 오른쪽 손주 노드 구조로 불균형해진 경우. 위 그림 5-1의 LR이라고 표기한 그림이 예시이다.
- RR(Right-Right): root 노드를 중심으로 오른쪽 자식 노드 → 오른쪽 손주 노드로 기울어져 불균형해진 경우. 위 그림 5-2의 RR이라고 표기한 그림이 예시이다.
- RL(Right-Left): root 노드를 중심으로 오른쪽 자식 노드 → 왼쪽 손주 노드로 기울어져 불균형해진 경우. 위 그림 5-2의 RL로 표기한 그림이 예시이다.
각각의 불균형한 경우에 대해 노드를 회전시켜 균형을 맞추는 방법은 다음과 같다.
- LL의 경우: root 노드의 왼쪽 자식 노드를 새로운 root 노드, 즉 new_root로 지정한다. (편의상 기존의 root 노드를 node라 지칭하겠다) 그러면 기존의 root 노드의 왼쪽 자식 노드의 왼쪽 자식 노드, 즉 왼쪽 손주 노드는 new_root의 왼쪽 자식 노드가 되고, 기존의 root 노드는 new_root의 오른쪽 자식 노드가 된다. 그 후, 기존 root 노드를 new_root보다 한 단계 아래에 위치하게끔 오른쪽(시계방향으로 약 90도)으로 회전한다. 그러면 균형을 맞출 수 있다. 이 과정에서 회전하기 전의 root 노드의 왼쪽 자식 노드(new_root로 지정될 노드)의 오른쪽 하위 트리는 회전 후의 node의 왼쪽 하위 트리로 지정한다. 이 모든 과정이 그림 5-1의 윗부분에서 묘사하고 있다.
- LR의 경우: 편의상 기존 root 노드를 node로 지칭한다. 그리고 node의 왼쪽 자식 노드의 오른쪽 자식 노드를 새로운 root 노드로 지정한다(new_root). 그 후, new_root를 왼쪽으로 회전시킨 후, new_root와 node의 왼쪽 자식 노드의 위치를 서로 뒤바꾼다. 그러면 LL과 같은 상황이 되는데, 이후는 LL인 경우와 똑같이 node를 오른쪽 아래로 회전시킨다. 이 모든 과정은 그림 5-1의 아래부분에 묘사되었으며, 이 과정에서 각 노드들의 하위 트리와의 새로운 연결 설정은 해당 그림을 유심히 주목하면 알 수 있다.
- RR의 경우: 기존의 root 노드를 node로 지칭하고, node의 오른쪽 자식 노드는 새로운 root 노드, new_root로 지정한다. 그 후, node를 왼쪽으로 회전시킨다. 이 과정은 그림 5-2의 윗부분에 묘사되어 있다. 각 노드들과 하위 트리간의 새로운 연결 설정도 해당 그림에 묘사되어 있다.
- RL의 경우: 기존의 root 노드를 node로 지정하고, 새로운 root 노드가 될 노드는 node의 오른쪽 자식 노드의 왼쪽 자식 노드로, 해당 노드를 new_root로 지정한다. new_root를 오른쪽으로 회전한 후, new_root와 node의 왼쪽 자식 노드의 위치를 서로 뒤바꾼다. 그 후, node를 왼쪽으로 회전시킨다. 이 과정은 그림 5-2의 아래 부분에서 묘사되고 있다. 회전 후의 각 노드들과 하위 트리들의 연결 관계도 해당 그림을 통해 볼 수 있다.
다음은 데이터 삽입 및 삭제 시 발생될 수 있는 불균형한 문제를 해결하기 위한 코드이다. 해당 코드는 AVL Tree 클래스 내에 또 다른 클래스의 형태로 정의하였다.
class AVLTree(BinaryTree):
"""
자가 균형 이진 트리 중 하나. 왼쪽 하위 트리와 오른쪽 하위 트리의 불균형을
스스로 탐지하고 이를 스스로 고쳐 균형을 유지한다.
"""
class SelfBalancingTools():
def solveWhenLeftLeaning(self, node: BNode) -> BNode:
"""
노드가 왼쪽으로 치우쳐져 있을 때 이를 고치는 메서드.
"""
if node.BalanceFactor() >= 2:
if node.leftChild.BalanceFactor() >= 0:
# Left-Left
node = self.__rotateRight(node)
else:
# Left-Right
node = self.__rotateLeftRight(node)
return node
def solveWhenRightLeaning(self, node: BNode) -> BNode:
"""
노드가 오른쪽으로 치우쳐져 있을 때 이를 해결하는 메서드.
"""
if node.BalanceFactor() <= -2:
if node.rightChild.BalanceFactor() <= 0:
# Right-Right
node = self.__rotateLeft(node)
else:
# Right-Left
node = self.__rotateRightLeft(node)
return node
def __recalculateDepthInSubTree(
self,
root_of_subtree: BNode,
increase: bool
) -> None:
"""
주어진 하위 트리의 루트 노드로부터 해당 루트 노드를 포함한
하위 트리의 모든 노드들의 depth 값을 조정하는 메서드. \n
매개변수)\n
root_of_subtree: 하위 트리의 루트 노드 객체. \n
increase: 하위 트리 내 모든 노드들의 depth값을 증가시킬지 감소시킬지
알려주는 매개변수. True -> 1씩 증가, False -> 1씩 감소.
"""
current_node = root_of_subtree
if current_node is None: return
self.__recalculateDepthInSubTree(
current_node.leftChild,
increase
)
self.__recalculateDepthInSubTree(
current_node.rightChild,
increase
)
if increase:
current_node.depth += 1
else:
current_node.depth -= 1
def __rotateRight(self, node: BNode) -> BNode:
new_root = node.leftChild
node.leftChild = new_root.rightChild
new_root.rightChild = node
new_root.depth -= 1
node.depth += 1
new_root.leftChild.depth -= 1
self.__recalculateDepthInSubTree(node.rightChild, True)
self.__recalculateDepthInSubTree(
new_root.leftChild.leftChild,
False
)
self.__recalculateDepthInSubTree(
new_root.leftChild.rightChild,
False
)
node.calculateNodeHeight()
return new_root
def __rotateLeftRight(self, node: BNode) -> BNode:
new_root = node.leftChild.rightChild
new_left = node.leftChild
new_left.rightChild = new_root.leftChild
node.leftChild = new_root.rightChild
new_root.leftChild = new_left
new_root.rightChild = node
new_root.depth -= 2
node.depth += 1
self.__recalculateDepthInSubTree(
node.rightChild,
True
)
self.__recalculateDepthInSubTree(
node.leftChild,
False
)
self.__recalculateDepthInSubTree(
new_left.rightChild,
False
)
node.calculateNodeHeight()
new_left.calculateNodeHeight()
return new_root
def __rotateLeft(self, node: BNode) -> BNode:
new_root = node.rightChild
node.rightChild = new_root.leftChild
new_root.leftChild = node
new_root.depth -= 1
node.depth += 1
new_root.rightChild.depth -= 1
self.__recalculateDepthInSubTree(
node.leftChild,
True
)
self.__recalculateDepthInSubTree(
new_root.rightChild.leftChild,
False
)
self.__recalculateDepthInSubTree(
new_root.rightChild.rightChild,
False
)
node.calculateNodeHeight()
return new_root
def __rotateRightLeft(self, node: BNode) -> BNode:
new_root = node.rightChild.leftChild
new_right = node.rightChild
node.rightChild = new_root.leftChild
new_right.leftChild = new_root.rightChild
new_root.leftChild = node
new_root.rightChild = new_right
node.depth += 1
new_root.depth -= 2
self.__recalculateDepthInSubTree(
node.leftChild,
True
)
self.__recalculateDepthInSubTree(
node.rightChild,
False
)
self.__recalculateDepthInSubTree(
new_right.leftChild,
False
)
node.calculateNodeHeight()
new_right.calculateNodeHeight()
return new_root
def __init__(self):
super().__init__()
self.solver = AVLTree.SelfBalancingTools()
먼저, 왼쪽으로 기울어졌는지 오른쪽으로 기울어졌는지를 탐지하고 이를 해결하기 위한 메서드인 solveWhenLeftLeaning(), solveWhenRightLeaning()를 정의한 후, 그 메서드 안에서 불균형한 각각의 경우에 대해 __rotate로 이름이 시작하는 서브 메서드들을 정의하여 그 안에서 해결하는 코드를 작성하였다. 그림 5-1, 5-2를 유심히 보면 알겠지만, 균형을 맞출 때 일부 노드와 하위 트리들의 높이, 깊이(depth)의 값이 달라짐을 알 수 있다. 이를 맞추기 위해, 깊이는 __recalculateDepthInSubTree() 메서드로 재조정하도록 하였고, 높이는 기존의 노드 객체에 있던 calculateNodeHeight()으로 재조정하도록 하였다.
자동으로 불균형을 감지하고 이를 균형으로 맞추도록 하는 기능을 데이터 삽입 메서드인 _insert()에는 다음과 같이 추가하였다.
class AVLTree(BinaryTree):
# (중략)
def _insert(
self,
node: BNode | None,
value: NodeValue
) -> BNode:
"""
self.insert() 메서드를 돕는 서브 메서드.
반환값은 node 매개변수로 대입된 루트 노드.
"""
if node is None: return BNode(value, self._node_depth)
self._node_depth += 1
if value <= node.value:
node.leftChild = self._insert(node.leftChild, value)
node.calculateNodeHeight()
node = self.solver.solveWhenLeftLeaning(node)
else:
node.rightChild = self._insert(node.rightChild, value)
node.calculateNodeHeight()
node = self.solver.solveWhenRightLeaning(node)
node.calculateNodeHeight()
return node
다음은 데이터를 삭제하는 _remove()와 이를 보조하는 _removeMin() 메서드에 위에서 구현한 기능을 적용한 예시이다.
class AVLTree(BinaryTree):
# (중략)
def _remove(
self,
node: BNode | None,
target_value: NodeValue
) -> BNode | None:
"""
self.remove() 메서드를 돕는 서브 메서드.
반환값은 매개변수 node. 단, 이 메서드를 실행하고 나면
구조가 바뀐 하위 트리를 가지게 될 것이다.
"""
if node is None: return None
if target_value < node.value:
node.leftChild = self._remove(node.leftChild, target_value)
node = self.solver.solveWhenRightLeaning(node)
elif target_value > node.value:
node.rightChild = self._remove(node.rightChild, target_value)
node = self.solver.solveWhenLeftLeaning(node)
else:
if node.leftChild is None:
self._num_node -= 1
if node.rightChild: node.rightChild.depth -= 1
return node.rightChild
if node.rightChild is None:
self._num_node -= 1
if node.leftChild: node.leftChild.depth -= 1
return node.leftChild
# 아래 코드는 삭제하고자 하는 노드가 두 자식 노드를
# 모두 가지고 있을 경우를 처리하는 코드임.
node_to_be_removed: BNode = node
depth_of_original = node.depth
# 삭제되어 사라질 노드 자리를 대체하기 위해
# 대체할 노드를 삭제할 노드의 오른쪽 하위 트리의
# 최소값을 가지는 노드로 가져와 대체한다.
# 이를 위해 우선 삭제할 노드의 오른쪽 노드를 먼저
# 가리켜야 한다.
node = node.rightChild
# 최소값을 가지는 노드는 왼쪽 자식 노드를 가지지 않는 노드이다.
# 해당 노드를 탐색한다.
while node.leftChild: node = node.leftChild
node.rightChild = self._removeMin(node_to_be_removed.rightChild)
# 삭제될 노드의 빈자리를 채우는 최소값 노드의 왼쪽 자식 노드는
# 삭제될 노드의 왼쪽 자식 노드를 가리키도록 한다.
node.leftChild = node_to_be_removed.leftChild
node.depth = depth_of_original
node = self.solver.solveWhenLeftLeaning(node) #1
self._num_node -= 1
node.calculateNodeHeight()
return node
def _removeMin(self, node: BNode) -> BNode | None:
"""
self._remove() 메서드를 돕는 서브 메서드.
최소값을 가지는 노드가 삭제될 노드 자리로 갈 때,
최소값을 가지는 노드의 빈자리를
최소값 노드의 하위 오른쪽 자식 노드로 대체.
반환값은 구조 조정을 마친 루트 노드.
"""
if node.leftChild is None: return node.rightChild
node.leftChild = self._removeMin(node.leftChild)
node.leftChild.depth -= 1
node = self.solver.solveWhenRightLeaning(node) #2
node.calculateNodeHeight()
return node
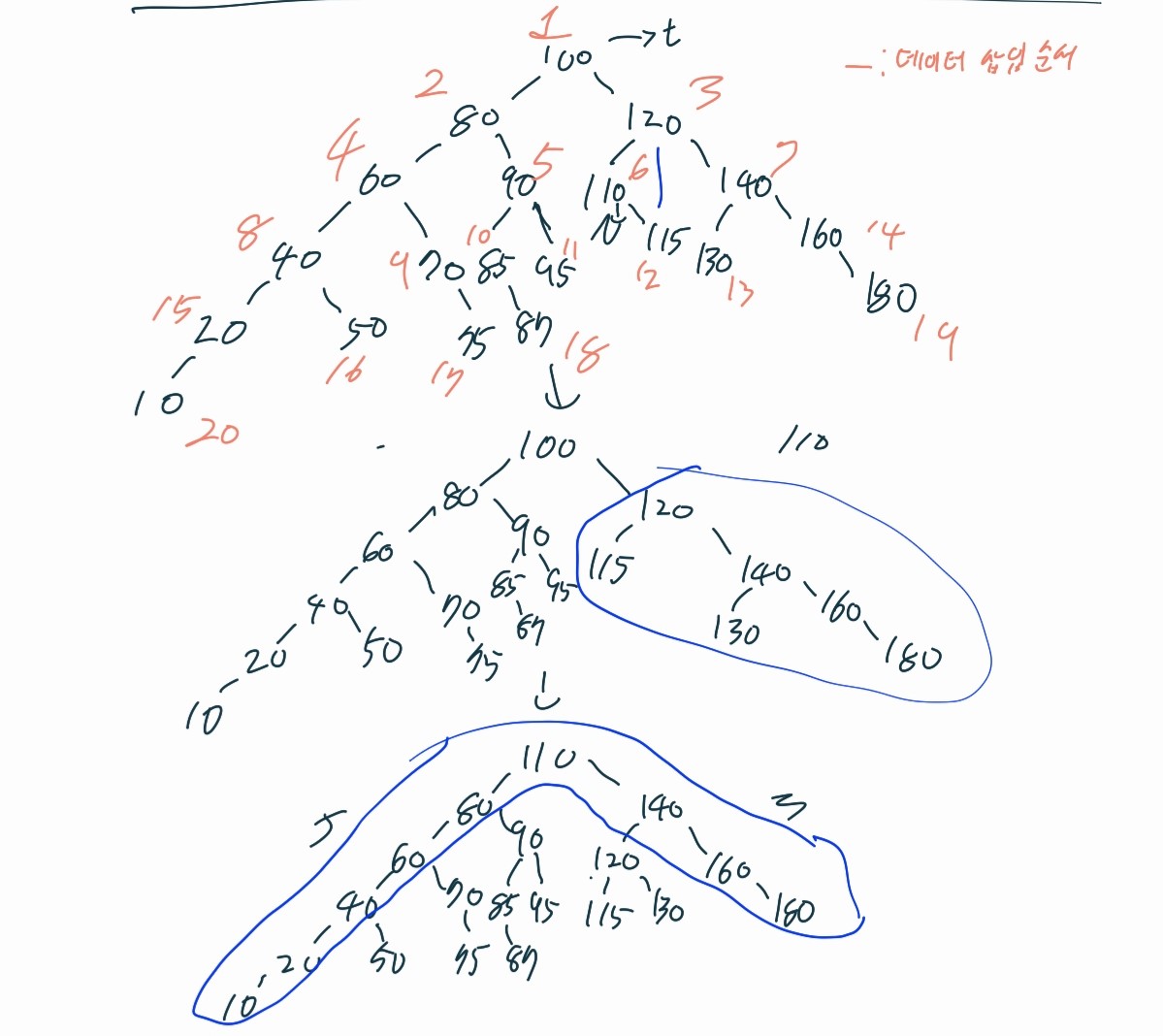
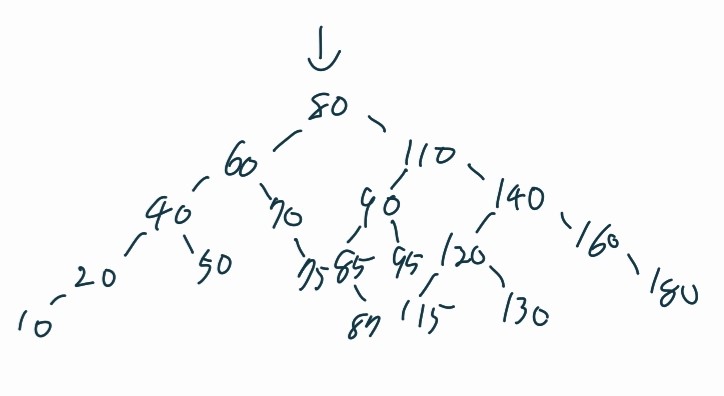
root 노드를 삭제할 때, 오른쪽 하위 트리 내에서 최소값을 가지는 노드를 가져와 빈 자리를 채우는 방식을 채택하였으므로, 이 과정에서 이진 트리가 전체적으로 왼쪽으로 기울 수 있다. 이를 위 예제 5-5의 #1에서 해결하였다. 또한, 삭제된 노드의 빈자리를 채우기 위해 오른쪽 하위 트리의 최소값을 떼어내고 그 빈자리를 해당 노드의 오른쪽 하위 트리의 root 노드로 채웠을 때, 기존 최소값 노드의 부모 노드의 관점에서 볼 때 오른쪽으로 기울 수도 있다. 이를 예제 5-5의 #2 에서 해결하였다.
참고로, 데이터 삭제 시 2번 연속으로 균형 재조정이 일어날 수 있다. 다음 그림은 그 예이다.
AVL Tree의 시간복잡도
균형을 재조정하는 기능 자체는 그 연산이 입력값의 크기에 상관없으므로 O(1)의 시간복잡도를 가진다. 이는 노드의 높이, 깊이를 계산하는 메서드도 마찬가지이다.
일반적인 이진 탐색 트리에 비해 AVL Tree에서는 모든 데이터가 오름차순, 또는 내림차순으로 입력되더라도 이를 조정하여 최대한 완전 이진 트리에 가깝게 구조를 재조정해준다. 따라서 최악의 경우, 데이터의 삽입 및 삭제, 그리고 검색의 시간복잡도는 O(log N)이 된다.
이진 트리의 다른 자료구조에서의 활용
이진 트리는 다음의 자료구조 구현에도 활용될 수 있다.
- 해시 테이블을 이진 트리로 구현할 수 있다. 이 때, 각 노드에는 키(키가 문자열일 경우 이를 해싱한 숫자값)와 값(value)을 담는 변수들이 존재한다. 이진 트리로 구현하면 기존의 해시 테이블에서는 불가능했던 키를 오름차순으로 반환하는 트리 순회 기능도 사용할 수 있게 된다.
- 우선순위 큐를 이진 트리로 구현할 수 있다. 이 때 각 노드에는 우선순위 값과 value를 담는 변수들이 존재한다. 기존의 배열에 데이터를 담는 방식의 힙 자료구조는 미리 값들의 개수들을 세어 그만큼 크기의 고정된 배열을 생성해야했다. 그러나 이진 트리는 그럴 필요없이 값이 추가될 때마다 동적으로 그 크기를 늘릴 수 있다. 또한, 힙 자료구조로 우선순위 큐를 구현하는 것에 비해 우선순위 값의 오름차순으로 값들을 추출해낼 수 있다는 장점이 있다(트리 순회 이용).
이 페이지에서 나온 예제 코드들의 풀버전은 다음의 링크에서 확인 가능하다. https://github.com/JeroCaller/ds-and-algo-in-python/tree/main/datastructures/binary_tree
Reference
[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)
[2]
AVL Tree Data Structure - GeeksforGeeks
[3]
[자료구조] 트리(Tree) 이진 트리(Binary Tree) 트리 순회 (Tree Traversal) (Python)
This content is licensed under
CC BY-NC 4.0


댓글남기기