[알고리즘] 이진 배열 탐색 (Binary array search)
이진 탐색은 숫자로 이루어진 크기 N을 가지는 입력값에서 특정 값을 찾기 위한 방법 중 하나로, 입력값들이 오름차순 또는 내림차순으로 정렬되어 있을 때, 한 번에 탐색 범위를 입력값 크기의 절반인 N/2로 한정하여 탐색하는 방법이다.
예를 들어 뚜껑이 닫힌 상자 7개가 있고, 각 상자에는 숫자 카드가 하나씩 있다고 가정해보자. 이 때 상자 뚜껑을 몇 번만 열면 원하는 숫자 카드를 찾을 수 있을까?
생각할 수 있는 간단한 방법은 맨 왼쪽 상자부터 원하는 숫자 카드가 나올 때까지 하나씩 뚜껑을 열어보는 것이다. 그런데 만약 맨 오른쪽에 원하는 숫자 카드가 있었다면 총 7번의 뚜껑을 열어야 하는 것이다. 만약 N개의 상자들이 존재했다면 최악의 경우 N번의 작업을 해야 하는 것이다.
그런데 만약 당신이 숫자 카드들이 오름차순(또는 내림차순)으로 정렬되어 있다는 사실을 안다면? 앞선 방법보다 더 효율적인 방법이 있다.
이진 탐색의 예
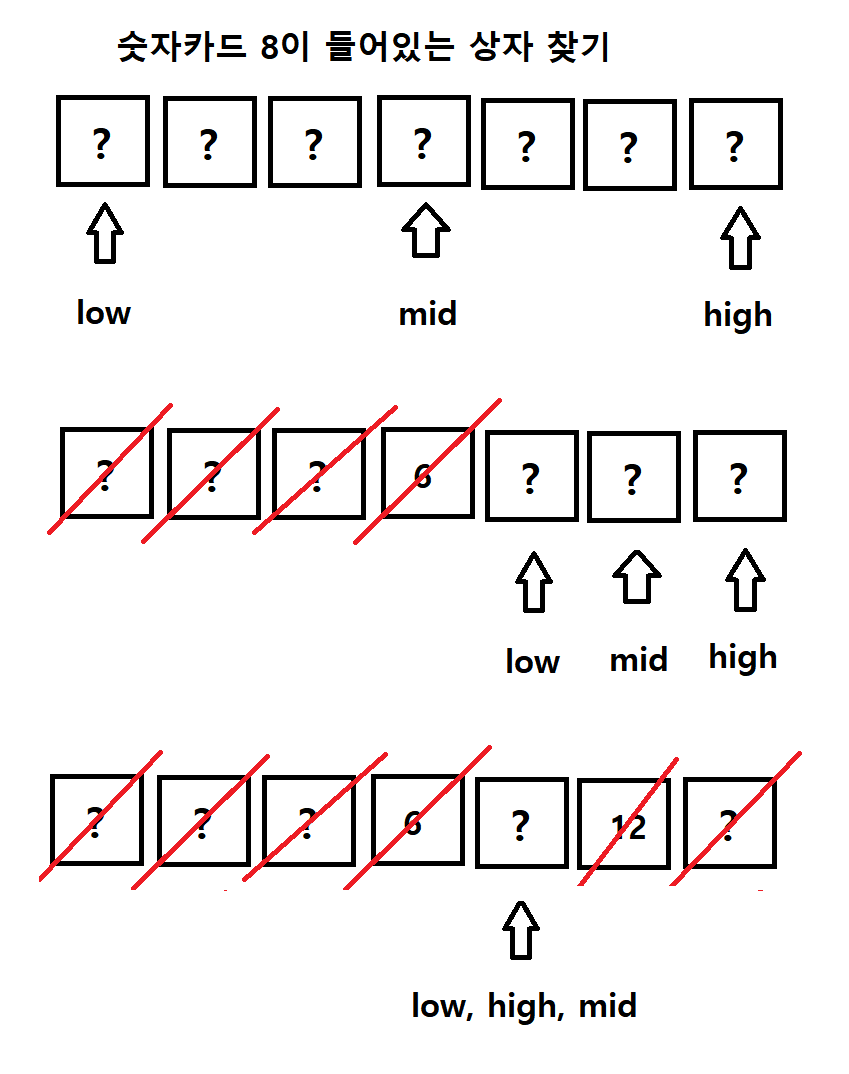
예로 위 사진에서처럼 숫자 카드 8을 찾는다고 해보자. 그러면 우선 맨 가운데에 위치한 상자를 열어본다. 그런데 열어보니 8이 아닌 6이 있었다. 여기서 6 < 8이고, 가운데에서 왼쪽에 있는 상자들은 전부 6보다 작은 숫자일테니 당연히 8은 그 영역에 없을 것이다. 그러므로 숫자 카드 6이 들어있던 가운데 상자를 포함하여 그 왼쪽에 있는 상자들은 모두 탐색 범위에서 제외한다. 그러면 오른쪽에 있던 3개의 상자가 남는다. 여기서도 똑같이 가운데에 위치한 상자를 연다. 열어보니 12가 들어있었다. 8 < 12이므로 숫자카드 12가 들어있는 상자를 포함하여 그 오른쪽에 있는 상자도 8보다 더 클 것이므로 해당 상자들은 탐색 범위에서 제외한다. 이제 남는 건 숫자 카드 12가 들어있던 상자의 왼쪽 상자 뿐이다. 해당 상자를 연다. 이 과정은 숫자 카드 8을 중간에 찾지 못하는 최악의 경우를 상정하였는데, 그럼에도 상자 뚜껑은 단 3번만 열어서 확인할 수 있었다. 앞서 맨 왼쪽에서부터 차례대로 열어 최악의 경우 7번을 열었던 것에 비하면 효율적이다.
입력값의 크기가 N인 배열이 이미 정렬되어 있을 때, 원하는 단 하나의 값을 찾기 위해 필요한 연산은 몇 번일까? 앞선 과정을 곰곰이 생각해보면, 단 1개의 값을 얻기 위해서 탐색 범위를 계속 절반으로 줄여왔다. 즉, 전체 크기 N을 2로 k번만큼 나눠야 했다. 이를 수식으로 다음과 같이 확인해볼 수 있다.
\[\frac{N}{2^k}=1 \\ N = 2^k \Leftrightarrow k = logN\]위 수식의 맨 첫째 줄은 N을 2로 k번 만큼 나누었을 때 단 1개의 결과값이 나와야 한다는 사실을 수식으로 표현한 것이다.
즉, 원하는 값을 찾기 위해 필요한 연산의 수 k는 log N과 같음을 알 수 있다. (여기서 log는 밑이 2인 로그로, 앞으로도 별 다른 언급이 없는 한 생략해서 표시할 것이다)
따라서, 맨 왼쪽부터 차례대로 값을 찾는 방법의 시간복잡도는 O(N)이라 할 수 있고, 이진 탐색의 시간복잡도는 O(logN)이라 할 수 있다. O(logN) < O(N)이므로 이진 탐색이 좀 더 효율적인 알고리즘임을 알 수 있다.
만약 N의 값이 2의 제곱수가 아니라면, k = log N의 값이 실수로 나올 것이다. 이 경우, 해당 실수보다 큰 정수 중 해당 실수에 가장 가까운 정수를 k로 택한다. (=실수의 정수부에 +1한 값을 취한다) 예) N = 7 → k = log 7 = 2.807 → k = 3
다음은 숫자값들이 이미 정렬되어 있는 리스트를 입력값으로 받아 이 중에서 원하는 값을 찾아 반환시켜주는 코드이다.
def binary_search_is_there(input_array: list[int], target_value: int) -> bool:
"""
이미 오름차순으로 정렬된 숫자값들로 이루어진 배열에서
target_value 매개변수로 명시된 값이 존재하는지를 찾는다.
"""
low = 0
high = len(input_array) - 1
while low <= high:
mid = (high + low) // 2
if target_value < input_array[mid]:
high = mid - 1
elif target_value > input_array[mid]:
low = mid + 1
else:
return True # 값을 찾았다.
return False # 찾는 값이 없다.
def find_index_binary_search(input_array: list[int], target_value: int) -> int:
"""
이진 탐색으로 찾고자 하는 값의 인덱스 반환.
존재하지 않으면 -1을 반환.
배열은 미리 오름차순으로 정렬되어 있어야 한다. \n
target_value: 배열 내에서 찾고자 하는 값.
"""
low = 0
high = len(input_array) - 1
while low <= high:
mid = (high + low) // 2
if target_value < input_array[mid]:
high = mid - 1
elif target_value > input_array[mid]:
low = mid + 1
else:
return mid # 값을 찾았다.
return -1 # 찾는 값이 없다.
if __name__ == '__main__':
data = [1, 2, 4, 6, 8, 12, 15]
find_value = 8
is_there = binary_search_is_there(data, find_value)
where_is_it = find_index_binary_search(data, find_value)
print(f"숫자 {find_value}은 존재하나요? {is_there}")
print(f"숫자 {find_value}의 인덱스는? {where_is_it}")
숫자 8은 존재하나요? True
숫자 8의 인덱스는? 4
만약 입력값의 크기 N이 짝수일 경우 위 코드에 따르면 mid가 정수로 딱 나오지 않을 것이다. 이 경우 N이 아닌 N - 1을 2로 나눈 값을 mid로 정해도 된다. 예를 들어 N = 8인 경우, 인덱스는 0부터 7이므로 mid = 7 / 2가 되므로, mid = 7 - 1 / 2 = 3 (4번째 값을 가리킴)으로 한다. 위 코드에서는 대신 나눗셈의 결과값의 정수부만 취하는 방식을 택했다.
Reference
[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)
This content is licensed under
CC BY-NC 4.0


댓글남기기