[알고리즘][그래프] Breadth first search (BFS, 너비 우선 탐색법)

Depth first search (DFS, 깊이 우선 탐색법) 페이지에서 살펴본 DFS는 여러 가능한 길들 중 하나를 골라 그 길을 우선 깊게 탐색하는 방식이었던 반면, BFS는 여러 가능한 길들을 한 칸씩 동시에 내딛어 탐색하는 방법이다. 즉, BFS는 source 노드로부터의 거리에 따라 같은 거리에 떨어진 노드들을 먼저 탐색하는 방식이다.

그림 1. BFS 탐색 과정을 표현한 그림.

한 쪽 길만 먼저 깊게 탐색하는 DFS와 다르게, BFS는 source 노드로부터 같은 거리에 떨어진 노드들을 모두 탐색한 다음, 바로 다음 칸에 해당하는 노드들을 탐색하는 방식으로 너비를 먼저 탐색하기에 이름도 “너비 우선 탐색”이라 붙여진 것으로 보인다.

source 노드로부터 가장 가까이 도달 가능한 곳에 존재하는 노드들을 먼저 기록한다. 그림 1을 예로 들면 (0, 1), (0, 3), (1, 2)가 되겠다. 그 후 차례대로 해당 노드들로 발을 내딛어 인접하고 미방문한 노드들을 기록한다. (0, 1)에서 미방문한 인접한 노드는 (0, 0)이므로 해당 노드가 기록될 것이다. 이 때에도 기록 순서가 중요한데, 아직 (0, 3), (1, 2)를 방문하지 않은 상태이므로 (0, 3), (1, 2), (0, 0)과 같이 기록한다. 그 다음 (0, 3)의 인접한 노드들 중 미방문한 노드는 (0, 4), (1, 3)이 있겠다. 이를 기록하면 (1, 2), (0, 0), (0, 4), (1, 3)가 될 것이다. 이번에는 (1, 2)를 탐색한다. 해당 노드에 인접한 미방문된 노드는 (2, 2)이므로 (0, 0), (0, 4), (1, 3), (2, 2)로 기록될 것이다. 이와 같은 과정을 반복한다.

기록 방식을 보면 알 수 있듯, 선입선출(FIFO)의 방식으로 기록해야 함을 알 수 있다. DFS가 스택 자료구조를 사용한 반면, BFS는 큐 자료구조를 사용하여 구현한다. 이는 source 노드로부터 거리가 d만큼 떨어진 노드들에 대해, d+1만큼 떨어진 노드들을 조사하기 전에 먼저 d만큼 떨어진 모든 노드들을 먼저 탐색해야 하기 때문이다.

다음은 BFS를 코드로 구현한 모습이다. 코드 구조 자체는 DFS와 거의 흡사하다.

# (생략)
from my_queue import DynamicQueue
# (생략)

class FindPathInMazeBFS(FindPathInMazeDFS):
    """
    너비 우선 탐색법(Breadth First Search)으로 미로의 입구부터 출구까지의 
    모든 경로 중 가장 짧은 경로를 찾는 클래스.
    """
    def __init__(
            self, 
            maze_g: nx.Graph, 
            maze_nodes_pos: PositionInfo,
            source_node: Node = None, 
            target_node: Node = None
        ):
        super().__init__(maze_g, maze_nodes_pos, source_node, target_node)
    
    def _search(self) -> NodeTrace:
        """
        넓이 우선 탐색법(Breadth-First Search)을 통해 미로의 입구부터 
        출구까지의 경로를 탐색. 
        스택 대신 큐를 사용하는 것을 제외하면 _DFS_Search 메서드에 사용된 
        방법, 코드가 거의 일치한다. 
        """
        visited: dict[Node, bool] = {}
        cp_nodes: NodeTrace = {}

        queue: DynamicQueue[Node] = DynamicQueue()
        visited[self.src] = True
        queue.enqueue(self.src)

        while not queue.isEmpty():
            node = queue.dequeue()
            for adjacent_node in self.G[node]:
                if adjacent_node not in visited:
                    cp_nodes[adjacent_node] = node
                    visited[adjacent_node] = True
                    queue.enqueue(adjacent_node)
        return cp_nodes

해당 코드에도 탐색 결과를 저장한 cp_nodes가 반환되는데, 해당 결과를 시각화하면 다음과 같다.

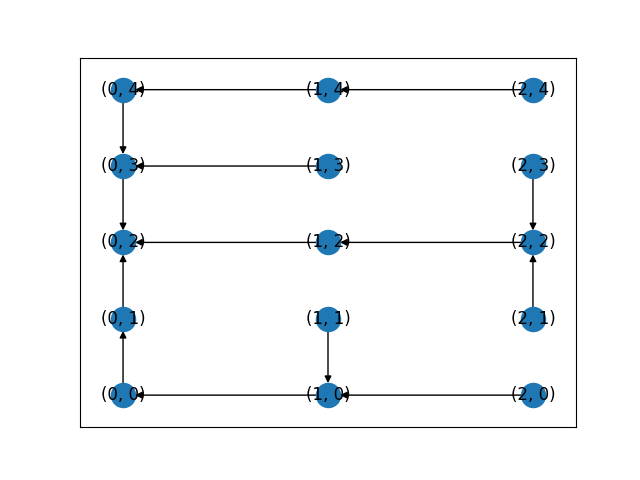
그림 2. BFS로 탐색한 결과

BFS 탐색법을 통해 얻은 자료를 바탕으로 출구로 향하는 경로를 구성하는 코드는 Depth First Search, DFS (깊이 우선 탐색) (그리고 backtracking) 문서의 예제 1-8을 그대로 이용하면 된다. 다음은 앞서 얻은 자료를 바탕으로 경로를 구성하여 이를 시각화한 그림이다.

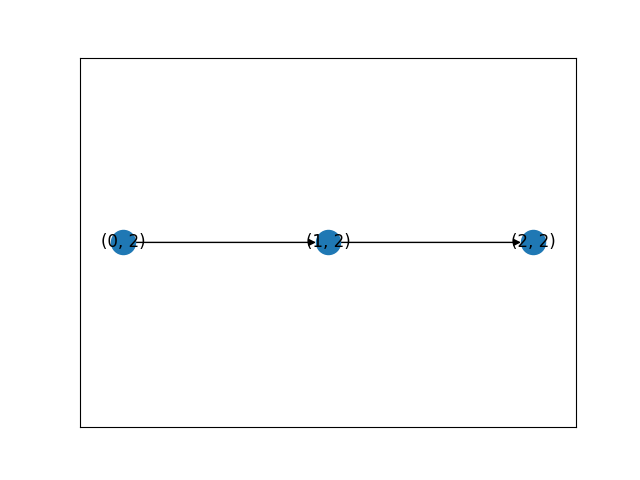
그림 3. BFS로 출구까지의 경로를 시각화한 그림.

예제 1-1의 큐에서 일어난 일을 다음과 같이 묘사하였다.

맨 왼쪽 끝 노드가 가장 먼저 꺼내지는(dequeue) 노드임.
queue

(0, 2)
(0, 3), (0, 1), (1, 2)
(0, 1), (1, 2), (0, 4), (1, 3)
(1, 2), (0, 4), (1, 3), (0, 0)
(0, 4), (1, 3), (0, 0), (2, 2)
(1, 3), (0, 0), (2, 2), (1, 4)
(0, 0), (2, 2), (1, 4)
(2, 2), (1, 4), (1, 0)
(1, 4), (1, 0), (2, 3), (2, 1)
(1, 0), (2, 3), (2, 1), (2, 4)
(2, 3), (2, 1), (2, 4), (1, 1), (2, 0)
(2, 1), (2, 4), (1, 1), (2, 0)
(2, 4), (1, 1), (2, 0)
(1, 1), (2, 0)
(2, 0)
None

BFS는 항상 최단 경로의 발견을 보장한다. 하지만 BFS는 보통 DFS에 비하면 항상 거의 모든 미방문한 노드를 방문해야 하므로 상대적으로 더 큰 저장용량이 필요하다. 물론 DFS도 최악의 경우 출구를 계속 찾지 못해 거의 모든 미로의 노드들을 방문해야할 때도 있겠지만, 이건 최악의 경우이고, BFS는 한 번에 모든 가능한 길들을 동시에 한 칸씩 방문하는 알고리즘이므로 당연히 상대적으로 (그리고 평균적으로) 더 많은 노드들을 방문해야 한다. 다음의 자료는 이를 방증하는 자료이다.

그림 4. 미로 탐색 알고리즘들의 비교. 회색으로 칠해진 원들은 출구로 향하는 경로를 의미하며, 파란색 원은 탐색을 위해 방문한 노드를 의미한다. Reference [1]을 참조함.

위 그림을 보면 알 수 있듯, BFS는 미로의 거의 모든 부분을 방문한다. 따라서 이를 기록하기 위한 저장 용량도 상대적으로 많이 필요함을 알 수 있다.

---

Reference

[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)

[2] [알고리즘][탐색] 너비탐색(BFS) & 깊이탐색(DFS)

This content is licensed under CC BY-NC 4.0