[알고리즘][그래프] Directed graph에서의 알고리즘들
개요
앞서 살펴본 그래프 탐색 알고리즘들, 가령 DFS, BFS 등도 directed graph에 사용할 수 있다. 단지 무향 그래프와 다르게, 유향 그래프에서는 u가 v로 접근할 수 있는 edge가 존재하지만 반대로 v 노드에서 u 노드로 접근 가능한 edge가 없을 수도 있다는 사실을 염두해둬야 한다.
Cycle
cycle은 유향 그래프에서 특정 노드 u에서 시작하여, 방향성을 갖는 edge를 따라 이동했을 때 도착하는 노드도 u인 경우를 의미한다. 즉, source 노드와 target 노드가 같고, 이 경로를 구성하는 edge들의 sequence라고 보면 된다. 유향 그래프에서 edge들의 방향을 따라 이동할 때 cycle에 걸리면 무한정 그 cycle을 계속 돌게 된다. (마치 무한 루프에 걸린 것처럼)
cycle의 예로 스프레트 시트가 있겠다. (흔히 쓰이는 엑셀이라고 보면 된다) 스프레트 시트의 각 칸에는 데이터를 직접 입력할 수 있을 뿐만 아니라, 다른 칸들의 데이터를 토대로 덧셈, 뺄셈 등의 여러 연산도 할 수 있는 기능이 있다. 해당 기능을 쓰기 위해선, 특정 칸에 = 부호로 시작하는 연산 공식 등을 적어야 한다. 이 기능을 사용할 경우 흔히 다른 칸을 참조할 때가 많다. 그런데 예를 들어, A1칸에는 “=A2”라 쓰고, A2 칸에는 “=A1”이라고 작성하면 이는 순환 참조(circular reference)가 되는데, 이는 에러의 일종이다. 이러한 에러를 방지하기 위해서 각 칸들을 그래프의 노드, 각 칸들이 다른 칸을 언급하는 것을 edge로 모델링한 후, 사용자가 데이터를 입력할 때마다 cycle을 감지하여 순환 참조 에러를 방지하도록 할 수 있겠다. (스프레드 시트에서의 “순환 참조”가 그래프로 모델링하면 “cycle”이 된다)
그래프에서 cycle의 존재 여부를 알기 위해서 DFS 탐색법이 쓰일 수 있다.
DFS를 이용한 cycle 탐지 알고리즘
DFS를 이용하여 cycle을 탐지하는 원리는 다음과 같다. DFS 탐색을 통해 탐색된 노드는 스택에 한 번 들어가게 된다. 스택에 한 번이라도 들어갔었던 노드를 따로 기록하는 변수를 정의하고 기록한다. 해당 변수를 in_stack이라고 하겠다. 이 때, 현재 탐색하는 노드가 이미 방문한 전적이 있으며, in_stack에 이미 존재하는 노드일 경우, 즉 스택에 이미 한 번 들어간 전적이 있는 노드가 또 탐색되었을 때 해당 경로가 cycle임을 알 수 있다. 이는 cycle을 따라 걷게 되면 cycle이 시작되는 노드를 두 번이나 밟게 될 수밖에 없다는 사실을 이용하는 것이다. (cycle이 아닌 경로를 걷게 되면 특정 노드를 두 번이나 밟을 수가 없다)
다음은 cycle이 포함된 그래프와 그 그래프를 탐색하며 cycle을 감지하는 과정을 묘사하였다.
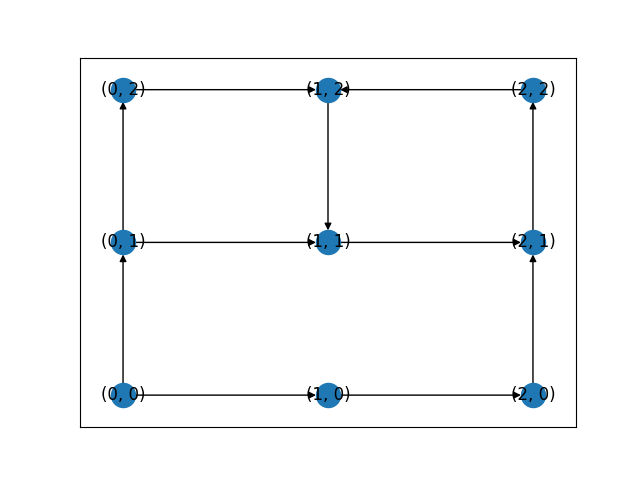
그림 1. cycle이 포함된 유향 그래프.
탐색 시작 노드가 (1, 1)인 경우.
현재 스택 내 노드 상황 | 스택에 들어왔던 노드 및 노드 방문 여부
(1, 1) | (1, 1): True
(2, 1) | (1, 1): True, (2, 1): True
(2, 2) | (1, 1): True, (2, 1): True, (2, 2): True
(1, 2) | (1, 1): True, (2, 1): True, (2, 2): True, (1, 2): True
(1, 1) | (1, 1): True, (2, 1): True, (2, 2): True, (1, 2): True
^^^^^^^^^^^^
(1, 1)이 이미 한 번 스택에 들어간 전적이 있음.
따라서 해당 경로는 cycle임.
해당 알고리즘을 코드로 구현할 때, cycle이 그래프의 어디에 존재하는지 모르므로, 사실상 그래프의 모든 노드들을 방문할수도 있다고 생각하고 구현해야 한다. 이는 부분적으로 연결되지 않은 그래프에 대해서도 적용된다. 다음의 경우를 보자.
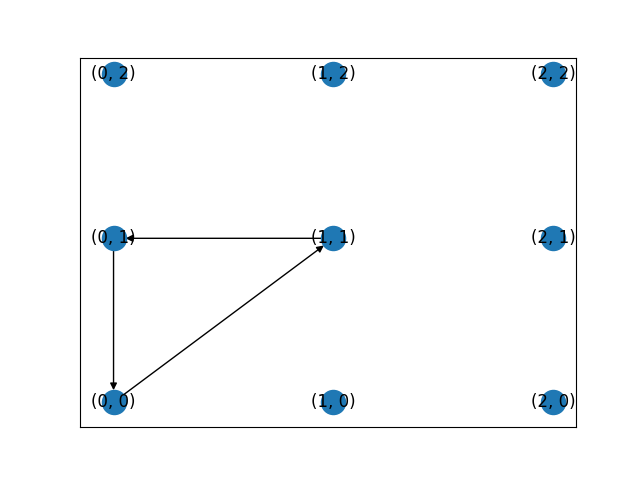
그림2. 비연결 그래프 예
그림 2의 경우, 특정 노드들이 삼각형을 이루는 edge들로 연결된 것을 제외하면 나머지 노드들은 edge가 존재하지 않는다. 따라서 만약 차수가 0인 노드부터 cycle 탐색을 실시하면, 연결된 edge가 없기에 이 경우 해당 그래프에 cycle이 없다고 판단할 것이다. 만약 이 검사를 모든 노드에 대해서 실행하지 않을 경우, 분명 cycle이 존재함에도 존재하지 않는다고 오판할 수도 있는 것이다. 따라서 그래프 내 cycle을 탐지하기 위해선 잠재적으로 모든 노드들을 방문할 수 있고, 즉 다른 탐색 시작점에서 다른 탐색 경로를 거칠 수 있다고 가정하고 코드를 구현해야 한다.
다음은 DFS를 이용한 cycle 탐지 알고리즘을 코드로 구현하기 전에, 우선 cycle 탐지기를 클래스로 정의한 모습이다.
import networkx as nx
import matplotlib.pyplot as plt
# type alias
# 노드의 (X, Y) 위치
PosX = int
PosY = int
Node = tuple[PosX, PosY]
Edge = list[tuple[Node, Node]]
PositionInfo = dict[Node, tuple[PosX, PosY]]
# (생략)
class CycleDetector():
"""
방향성 그래프(directed graph)에 cycle(순환 루트)이 존재하는지 검사하는 클래스.
"""
def __init__(self, directed_graph: nx.DiGraph):
self._dg = directed_graph
@property
def DG(self) -> (nx.DiGraph): return self._dg
@DG.setter
def DG(self, new_dg: nx.DiGraph): self._dg = new_dg
다음은 DFS 탐색법을 통해 그래프에 cycle이 존재하는지를 감지하는 코드이다. 위 예제 1-1의 클래스에 인스턴스 메서드로서 이어서 쓰면 된다.
def hasCycle(self) -> (bool):
"""
그래프에 cycle (순환 노드)이 있는지 확인하는 메서드.
존재하면 True, 그렇지 않으면 False 반환.
"""
visited: dict[Node, bool] = {}
in_stack: dict[Node, bool] = {}
def dfs(u: Node): #1
visited[u] = True #3
# 재귀 호출 스택에 포함되어 있는 노드들을 기록.
# 해당 노드가 재귀 호출 스택에 있다면 해당 노드의 값을
# True로 설정.
# 만약 해당 노드가 더 이상 재귀 호출 스택에 없다면
# 해당 노드의 값을 False로 설정.
in_stack[u] = True #2
for v in self._dg[u]:
if v not in visited:
if dfs(v): #4
# 한 루트만 파고든다.
# 현재 탐색하고 있는 루트가 순환 루트를 이루는지 검사.
# 순환 루트인 경우 True 반환.
return True
else:
if v in in_stack and in_stack[v]: #5
# 노드 v가 이미 방문한 것으로 표시되어 있을 때
# (visited[v] = True),
# 해당 노드가 아직 재귀 호출 스택에 존재할 수도 있다.
# 만약 그러한 경우, cycle이다.
return True
in_stack[u] = False #6
return False
위 예제 1-2의 #6으로 표시된 코드를 보면, 어떤 경로를 탐색할 때 해당 경로가 cycle이 아닌 경우, 탐색 시작 노드인 u의 in_stack[u]를 False로 지정한다. 이는 탐색하던 경로가 cycle이 아님을 판단하고 다른 경로로 탐색할 때 해당 노드가 또 탐색 경로에 포함될 수 있다. 이 때 해당 값을 True인 채로 남기면 해당 탐색 경로를 cycle로 오인할 수 있으므로 False로 지정하는 것이다.
위 예제 1-2은 cycle의 존재여부만을 알 수 있다. 만약 cycle의 경로까지 알고 싶다면 다음의 코드를 이용하면 되겠다.
def findCycle(self) -> (list[Node] | list):
"""
그래프에서 cycle을 찾고 해당 cycle의 경로를 반환.
"""
visited: dict[Node, bool] = {}
in_stack: list[Node] = []
def dfs(u: Node):
visited[u] = True
in_stack.append(u)
for v in self._dg[u]:
if v not in visited:
result = dfs(v)
if result != []:
return result
elif v in (visited and in_stack):
start_idx = in_stack.index(v)
end_idx = len(in_stack) - 1
cycle_list = in_stack[start_idx:end_idx+1]
cycle_list.append(v)
return cycle_list
in_stack.remove(u)
return []
for u in self._dg.nodes():
if u not in visited:
result = dfs(u)
if result != []:
return result
return []
그림 1과 같은 그래프가 주어졌을 때 hasCycle()과 findCycle()의 결과는 각각 다음과 같다.
True
[(1, 2), (1, 1), (2, 1), (2, 2), (1, 2)]
위상 정렬 (topological sort)
위상 정렬은 비순환 방향 그래프(Directed Acyclic Graph, DAG), 즉 cycle이 존재하지 않은 그래프의 노드들을 연결된 엣지들의 방향이 왼쪽 또는 오른쪽 한 방향으로만 향하게 선형으로 정렬하는 것을 말한다.
위상 정렬을 구현하는 코드는 앞서 살펴본 cycle 감지 알고리즘의 코드와 그 구조가 비슷하다. 다음은 비순환 방향 그래프를 위상 정렬해주는 코드이다.
def topological_sort(dg: nx.DiGraph):
"""
위상 정렬.
cycle이 존재하지 않는 방향성 그래프를 선형으로 정렬한다.
이 때 노드 간 edge의 방향은 항상 오른쪽으로 향하도록 한다.
문제점)
edge가 하나도 없는 노드에 대해서도 결과에 포함되어서
마치 해당 노드에 edge가 있는 것처럼 착각할 수도 있다.
"""
visited: dict[Node, bool] = {}
result: list[Node] = []
def dfs(u: Node):
visited[u] = True
for v in dg[u]:
if v not in visited:
dfs(v)
# out-degree = 0인 마지막 노드를 먼저 리스트에 삽입.
result.append(u)
for u in dg.nodes():
if u not in visited:
dfs(u)
result.reverse() # out-degree = 0인 노드를 맨 오른쪽 끝에 오도록 함.
return result
다음은 특정 그래프와 그 그래프를 토대로 한 위상 정렬 결과이다.
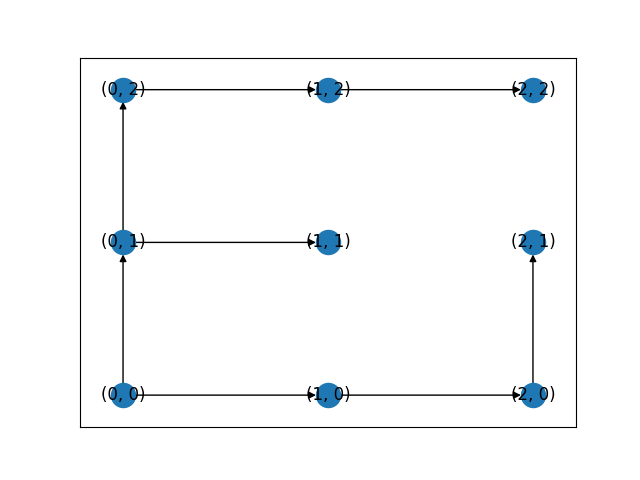
그림3. 위상 정렬을 위한 그래프 예시
[(0, 0), (1, 0), (2, 0), (2, 1), (0, 1), (1, 1), (0, 2), (1, 2), (2, 2)]
위상 정렬의 시간복잡도를 따져보면, 우선 거의 모든 노드들을 dfs()로 탐색하여 재귀 호출 스택에 한 번은 들어온다. 그리고, 특정 노드의 인접 노드에까지 한 번씩 접근한다 (무방향 그래프일 때는 총 2 * E번 방문하나, 방향 그래프에서는 일방통행이라 가정하면 총 E번 방문한다). 탐색한 노드를 리스트에 추가하는 연산은 O(1)의 성능을 가진다. 따라서 위상 정렬의 시간복잡도는 O(N+E)이다.
위에서 소개한 코드들의 풀버전 링크 : https://github.com/JeroCaller/ds-and-algo-in-python/blob/main/algorithms/graph/direct_graph.py
Reference
[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)
[2] 위상 정렬(Topological sort) 개념 및 구현
This content is licensed under
CC BY-NC 4.0


댓글남기기