[알고리즘][그래프] A* 알고리즘 & Greedy Best-first search

2023-07-25 10 분 소요

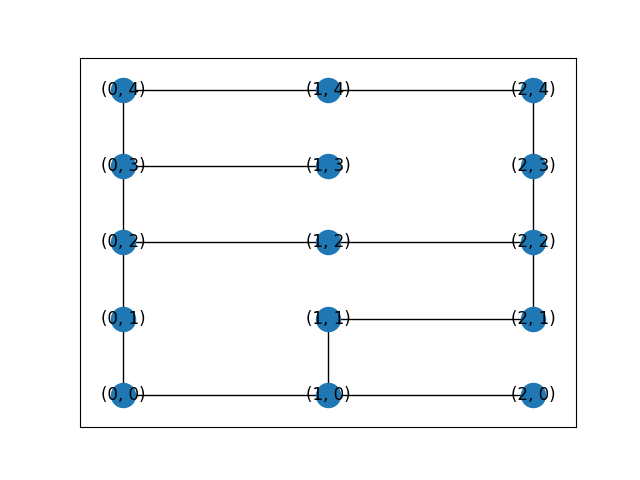
그림1. 미로를 무향 그래프로 나타낸 예시.

정보를 이용하여 미로 문제 풀기

앞서 살펴본 DFS와 BFS는 모두 source 노드와 target 노드의 위치라는 정보를 활용하지 않았다. 하지만 다음에 설명할 알고리즘은 해당 위치 정보들을 활용하여 미로 문제를 푼다.

시작은 source 노드에서부터 시작한다. 해당 노드의 인접한 노드들 중 미방문한 노드들을 조사한다. 그리고 그 인접한 노드들 모두 각각 target 노드와의 거리를 계산한다. 여기서는 맨하탄 거리 (Manhattan distance) 측정법을 이용한다. 해당 방법은 특정 노드의 위치가 (x1, y1)이고 target 노드의 위치가 (x2, y2)라 할 때, 두 노드 사이의 거리를 |x2-x1| + |y2-y1|으로 계산하는 방법이다. 그림 1을 예시로 들면, (0, 2)를 source 노드라 할 때 인접하고 미방문한 노드들 (0, 1), (1, 2), (0, 3)이 나올 것이다. 그러면 해당 노드들의 맨하탄 거리를 계산한다. (0, 1)을 예로 들면, target 노드를 (2, 2)라 할 때, d = |2-0| + |2-1| = 3이 된다. 이러한 계산을 모두 실행한다면 각각 (0, 1)→3, (1, 2)→1, (0, 3) → 3이 나온다. 이들 중 맨하탄 거리의 수치값이 가장 작은 노드 (1, 2)로 향한다. 해당 노드에서도 인접한 노드들 중 미방문한 노드들을 조사하고, 똑같이 인접 노드들에 대해 맨하탄 거리를 계산하여 같은 과정을 반복한다.

위 과정을 보면 알 수 있듯, 해당 알고리즘은 특정 노드와 target 노드와의 거리를 계산하여 가장 거리가 짧은 노드 쪽으로 걷게 만드는 방식임을 알 수 있다.

이 알고리즘을 구현하기 위해서는 우선순위 큐 자료구조가 필요하다. 각 노드들의 맨하탄 거리를 우선순위 값으로 지정하여 해당 우선순위 값이 가장 작은 노드를 꺼내어 작업을 수행하도록 하면 된다. max heap 방식을 이용한다면 거리가 가장 작은 노드가 우선시 되어야 하므로 각 노드들의 맨하탄 거리값의 앞에 마이너스 부호를 붙인다. min heap 방식을 이용한다면 어차피 우선순위 값이 가장 작은 노드가 먼저 dequeue되므로 마이너스 부호를 붙이지 않아도 된다.

해당 알고리즘의 코드 구조는 앞서 살펴본 DFS, BFS와 매우 유사하다. 단지 이번에는 맨하탄 거리를 측정하는 함수와, 탐색법에 우선순위 큐 자료구조를 사용한다는 것이 차이점이다. 다음은 해당 알고리즘을 max heap 기반 우선순위 큐를 이용하여 코드로 구현한 모습이다.

# (생략)
from priorityqueue import PriorityQueue
# (생략)
class FindPathInMazeGuided(FindPathInMazeDFS):
    """
    Guided Search 방법을 이용하여 미로의 입구에서부터 출구로 이르는 경로를 
    찾는 클래스.
    """
    def __init__(
            self, 
            maze_g: nx.Graph, 
            maze_nodes_pos: PositionInfo,
            source_node: Node = None, 
            target_node: Node = None
        ):
        super().__init__(maze_g, maze_nodes_pos, source_node, target_node)

    def _calculateDistance(
            self, 
            start_node: Node,
            end_node: Node
        ) -> int:
        """
        시작 노드에서 도착 노드까지의 거리를 구하고 반환하는 메서드. 
        시작 노드와 도착 노드의 각각 X좌표와 Y좌표끼리 뺀 값들을 더한 값이 
        거리이다. 
        """
        dx = abs(start_node[0] - end_node[0])
        dy = abs(start_node[1] - end_node[1])
        return dx + dy

    def _search(self) -> NodeTrace:
        """
        Guided Search 방법을 이용하여 모든 가능한 경로를 구하는 메서드. 
        DFS, BFS의 _search 메서드 내 코드 구조가 거의 동일하나, 여기서는 
        max binary heap에 기반한 priority queue를 사용한다. 
        우선순위는 각 노드마다 시작 노드에서 도착 노드까지의 거리(행 + 열)를 
        구한 값에 마이너스 기호를 붙인 값을 우선순위 값으로 함.  
        이러한 방식을 통해 최대한 거리가 짧은 경로를 추적하게끔 함. 
        (하지만 그렇다고해서 항상 최단 경로만을 찾는 것을 보장하지는 않는다고 함)
        """
        visited: dict[Node, bool] = {}
        cp_nodes: NodeTrace = {}

        pq: PriorityQueue[Node] = PriorityQueue()
        visited[self.src] = True
        distance = self._calculateDistance(self.src, self._target)
        pq.enqueue((self.src, -distance))

        while not pq.isEmpty():
            node = pq.dequeue()
            for adjacent_node in self.G[node.value]:
                if adjacent_node not in visited:
                    cp_nodes[adjacent_node] = node.value
                    visited[adjacent_node] = True
                    distance = self._calculateDistance(
                        adjacent_node, self._target
                    )
                    pq.enqueue((adjacent_node, -distance))
        return cp_nodes

위 코드의 풀버전을 보고자 한다면 다음의 링크를 참조. https://github.com/JeroCaller/ds-and-algo-in-python/blob/main/algorithms/graph/draw_maze.py

위 코드는 Depth First Search, DFS (깊이 우선 탐색) (그리고 backtracking) 문서에서 예시로 작성한 모듈 내에서 이어서 작성한 것이다. DFS와 유사한 모습들이 많기에 DFS 알고리즘을 구현한 클래스를 상속받아서 추가적인 코드 작성을 방지하였다.

위 예제 1-1도 DFS 때와 마찬가지로, 우선순위 큐 자료구조 내에 데이터가 모두 없어져 빌 때까지 작업을 수행하도록 하였다. target 노드에 도달하자마자 while 문을 빠져나가도록 코드를 수정하여 굳이 모든 미로를 탐색하지 않아도 되게끔 할 수도 있다.

위 알고리즘을 통해 얻은 인접 리스트의 시각화 그래프와 출구까지의 경로 그래프는 각각 다음과 같다.

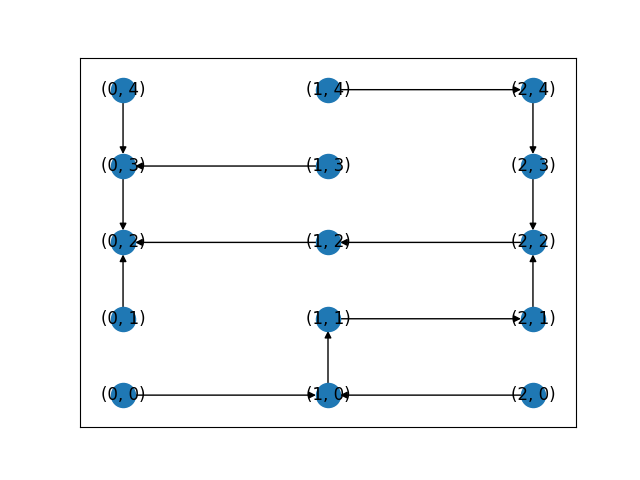
그림 2. 예제 1-1을 통해 얻은 인접리스트의 시각화 그림. 모든 노드들을 방문하도록 하면 어떤 모습일지에 대해 확인하기 위해 일부러 모든 노드들을 방문하도록 하였다. 앞서 말했듯, target 노드에 도착하면 바로 while문을 빠져나가도록 코드를 수정한다면 굳이 모든 노드들을 방문할 필요가 없어진다.

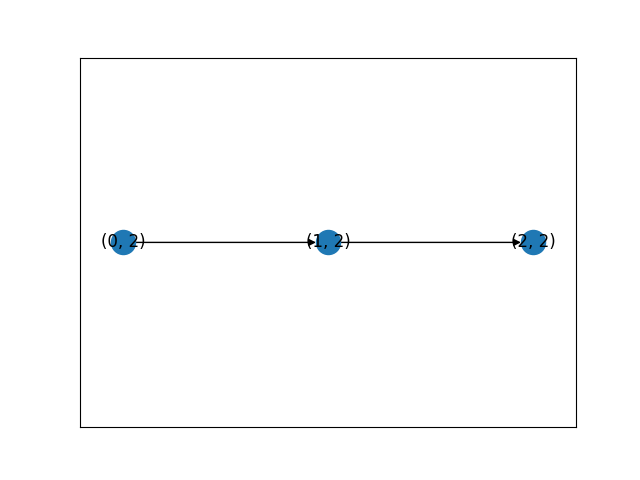
그림 3. 에제 1-1의 알고리즘을 이용하여 경로를 시각화한 그림.

위 알고리즘을 이용하여 미로 경로를 얻어낸 다른 그림을 DFS, BFS 탐색법을 이용해 푼 그림과 비교해보겠다.

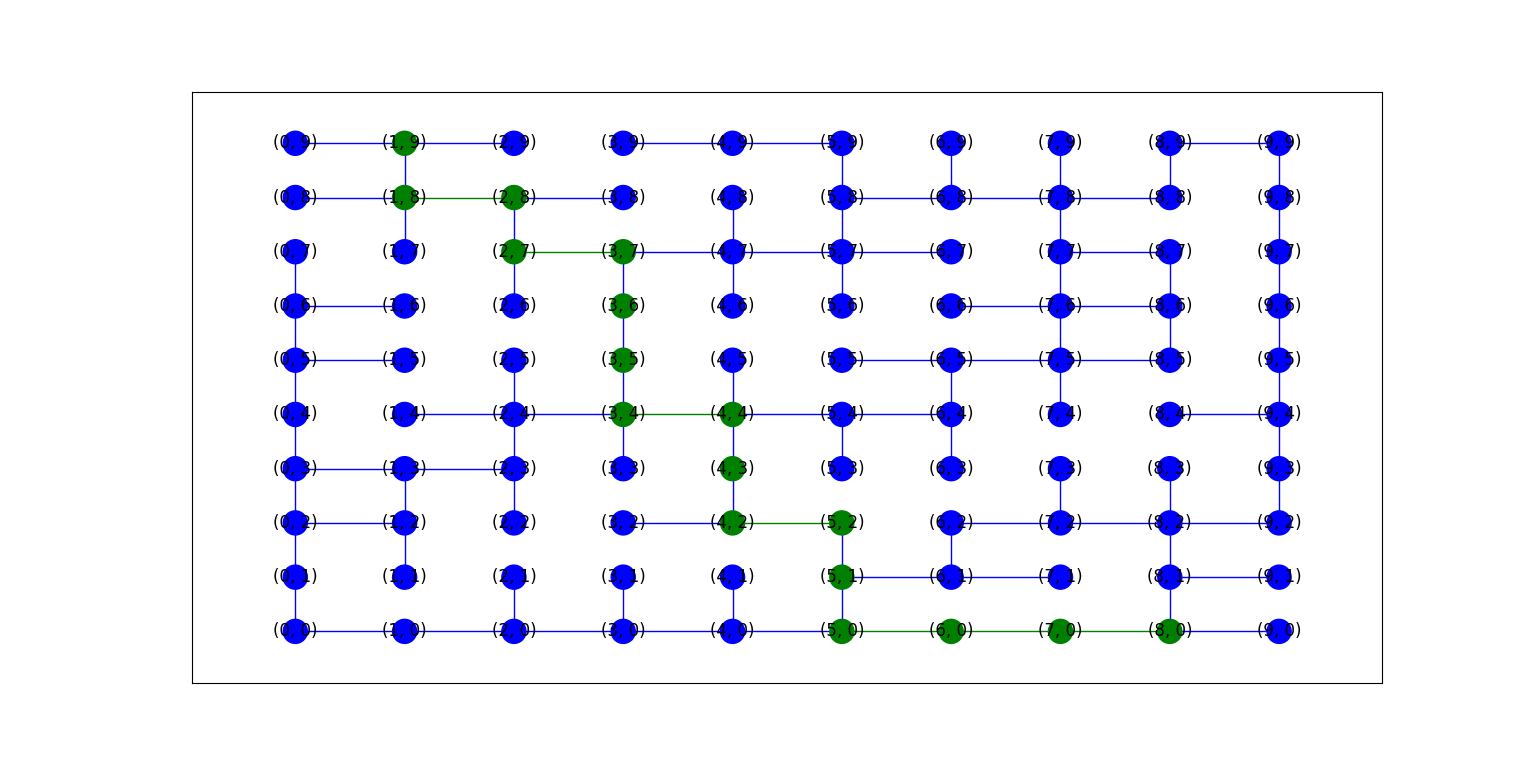
그림 4-1. 다른 미로에서 위에서 설명한 알고리즘을 이용하여 탐색해낸 경로를 시각화한 모습

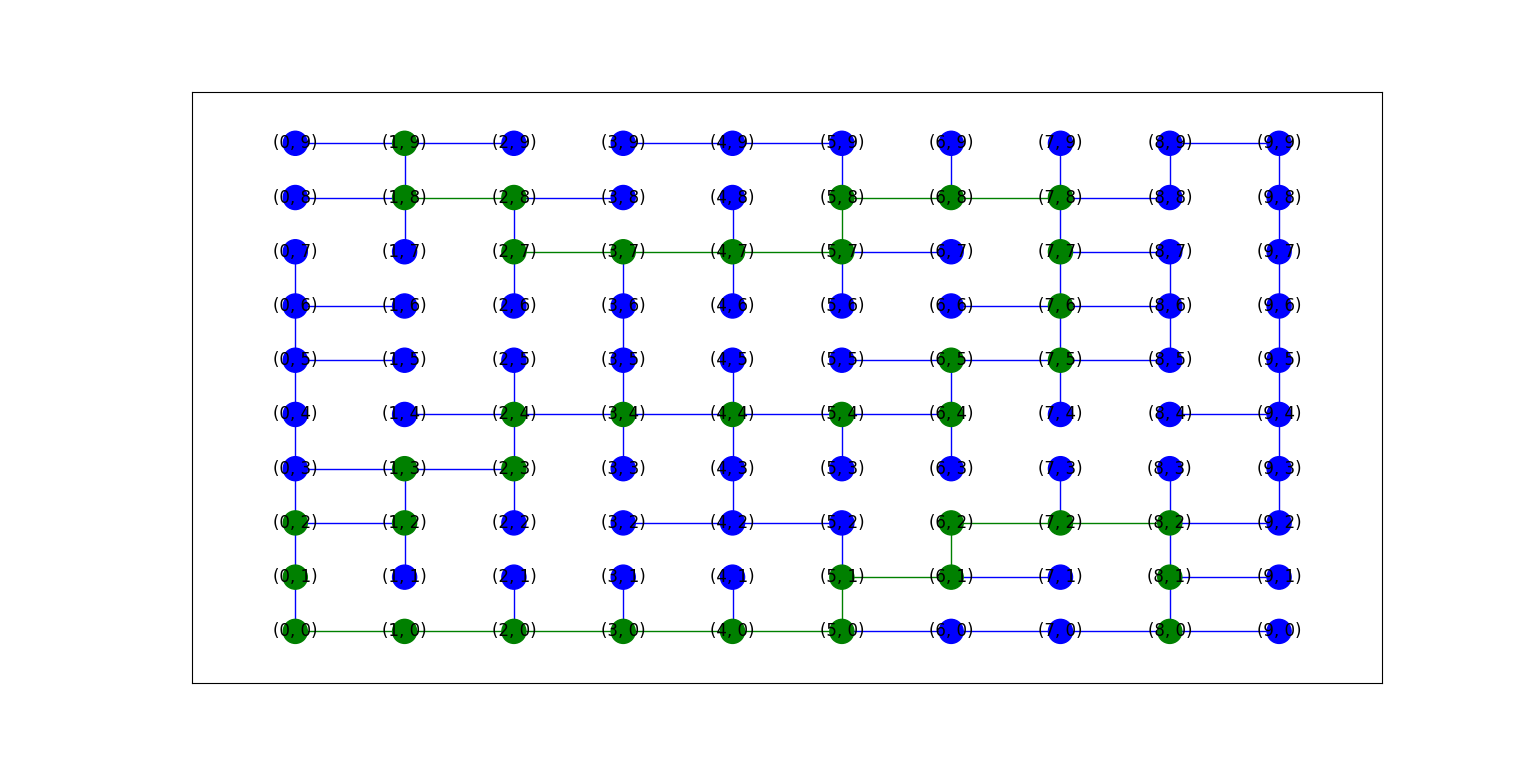
그림 4-2. 같은 그림을 DFS 탐색법을 이용하여 얻은 경로를 시각화한 모습

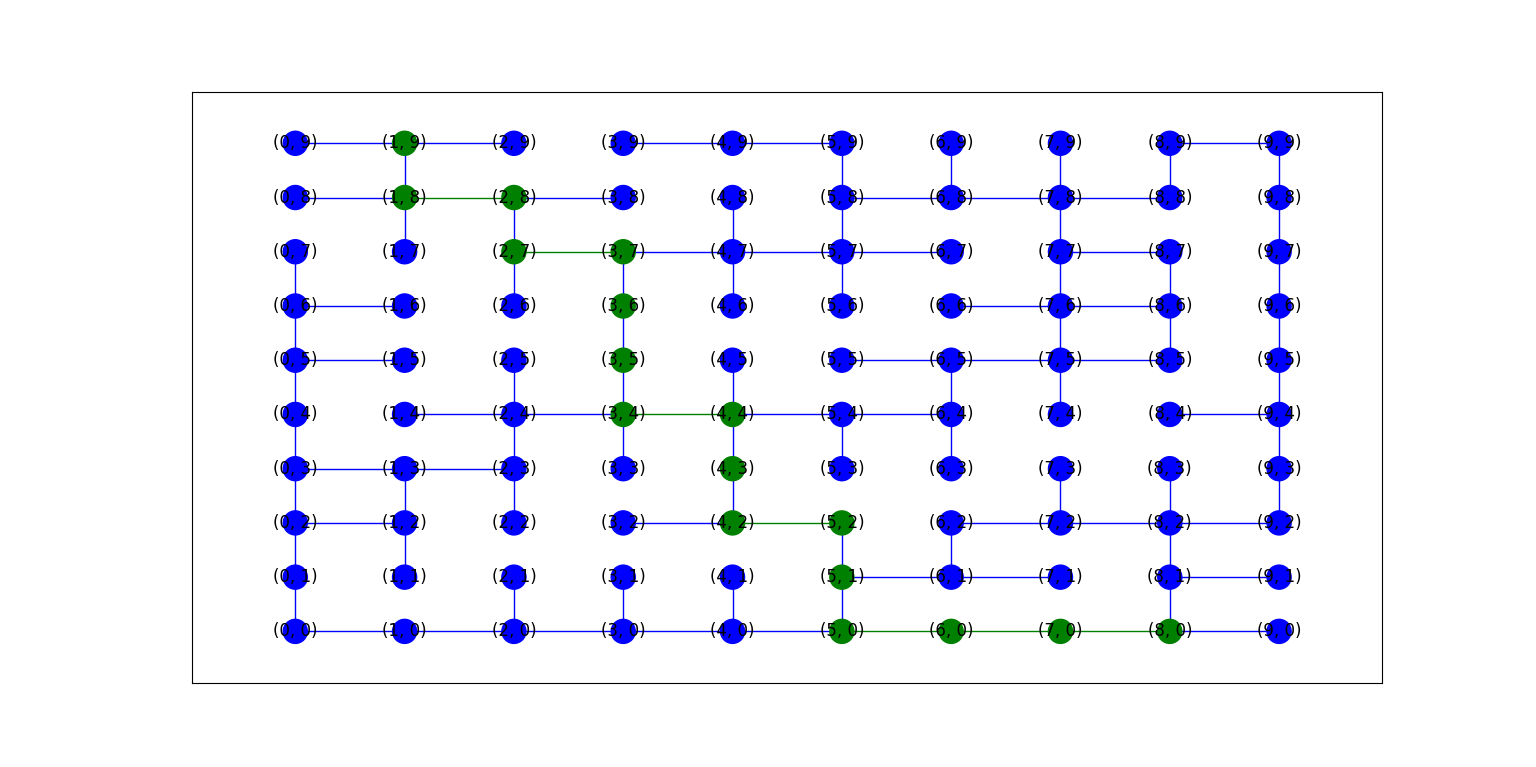
그림 4-3. 같은 그림을 BFS 탐색법을 이용하여 얻은 경로를 시각화한 모습

Uninformed search VS informed search

이전 페이지들에서 살펴본 DFS와 BFS 알고리즘은 오로지 현재 노드에서 인접한 노드들의 정보만을 알며, 그 이외의 정보, 가령 target 노드의 위치는 모르는 상태로 그래프를 탐색했다. 이와 같은 특성때문에 해당 알고리즘들을 Uninformed search 또는 blind search라 한다. 반면, 현재 노드에서 target 노드까지의 거리, 경로 비용 등의 외부적인 정보를 활용하는 그래프 탐색 알고리즘을 informed search 또는 heuristic search라 한다. informed search에는 greedy best-first search와 A* 알고리즘(”에이스타”라고 읽는 것 같다)이 존재한다. informed search은 모두 evaluation function (평가함수) f(n)과 휴리스틱 함수(heuristic function) h(n)을 이용한다.

Evaluation function & heuristic function

휴리스틱 함수는 현재 노드에서 target 노드까지의 거리 또는 그 거리를 이동하는데 드는 비용을 추정하는 함수로, 앞서 미로 찾기에서 사용한 맨하탄 거리 공식이 그 예이다. 휴리스틱 함수는 어떤 문제를 풀 때, 그 문제에 대한 정확한 해결책이 존재하지 않거나, 존재하더라도 문제를 푸는 시간이 너무 오래걸릴 때 대신 추정치로써 사용하는 것으로, 실제값과 정확하다는 보장이 없다.

평가함수에는 이러한 휴리스틱 함수만 들어가는 경우도 있으나, 또 다른 요소도 포함되는 경우가 있는데, 그것이 g(n) 함수이다. 해당 함수는 초기 노드에서 현재 노드까지 움직이는 데에 든 실제 비용을 의미한다. (해당 함수를 부르는 용어가 따로 있는지는 아직 모르겠다)

f(n), g(n), h(n)에서 괄호 안의 n은 특정 노드 n을 의미하며, 해당 함수들 모두 “특정 노드 n에 대한 함수값”이라 보면 된다.

평가함수 f(n)은 g(n), h(n)과 연관이 있으며, 둘 중 하나의 함수를 제외시킨다든가 둘 다 포함하느냐에 따라 서로 다른 알고리즘이 된다.

f = g + h일 경우: A* 알고리즘
f = h일 경우: greedy best-first search
f = g일 경우: dijkstra’s algorithm (다익스트라 알고리즘)

즉, A* 알고리즘에서 g(n) 함수가 제외되면 해당 알고리즘은 greedy best-first search로 환원되고, A* 알고리즘에서 h(n) 함수가 제외되면 해당 알고리즘은 dijkstra’s algorithm이 된다. 주의할 점은 다익스트라 알고리즘의 평가함수에는 휴리스틱 함수가 포함되지 않으므로, 해당 알고리즘은 informed search가 아니다. 여기서는 informed search에 대해서만 다룰 것이므로 A* 알고리즘과 greedy best-first search에 대해서만 다룰 것이다. (다익스트라 알고리즘은 다른 문서에서 다룰 예정)

앞서 미로 문제를 풀 때에는 맨하탄 거리라는 휴리스틱 함수만 사용하였고, 그 이전까지의 거리는 고려하지 않았으므로 greedy best-first search를 이용한 것이다.

앞서 언급한 알고리즘들은 f의 값이 가장 최소가 되는 경로를 향해 탐색해나간다. (그래서 우선순위 큐 자료구조가 필요하다)

A* 알고리즘

Heuristic function의 특성

휴리스틱 함수의 값이 항상 실제값과 같다거나, 아니면 최소한의 비용을 항상 계산해주는 건 아니다. 그러나, 만약 휴리스틱 함수의 추정값이 실제값과 동일하거나 더 낮으면 이를 admissible(”허용 가능한”이란 뜻같다)하다고 한다. 이를 수식으로 표현하면, h(n)을 휴리스틱 함수값으로 나온 비용, h*(n)을 실제 비용이라 한다면, 다음의 수식을 만족하면 휴리스틱 함수는 admissible하다고 한다.

\[h(n) \le h^*(n)\]

만약 휴리스틱 함수가 admissible한다면, 해당 휴리스틱 함수를 사용하는 알고리즘은 최적의 답을 보장한다. 즉, 미로로 말하자면, 항상 최단 경로를 보장한다. 따라서 A* 알고리즘을 이용할 때 admissible한 휴리스틱 함수를 사용한다면 A* 알고리즘은 최단 경로를 보장한다.

그런데, 휴리스틱 함수의 추정값이 실제값보다 더 낮은 경우, 최단 경로를 보장하나, 그만큼 정답을 찾는 시간이 느려진다고 한다 (이는 더 많은 노드들을 탐색해야 하기 때문이라고 하는데 추정값이 더 낮음에도 왜 더 많은 노드들이 탐색되는지는 아직 모르겠다). 만약 휴리스틱 함수의 추정값이 실제값과 똑같다면, 해당 알고리즘은 항상 최적의 경로로만 탐색하고 그 외의 경로는 탐색하지 않기에 탐색 속도가 빨라진다고 한다. (하지만 이런 경우는 그렇게 많이 있진 않을 것이다) 반대로 휴리스틱 함수의 추정값이 실제값보다 크다면, (즉, not admissible하면) 최단 경로를 찾는다는 보장은 없지만 대신 탐색속도가 빨라진다. 따라서, (휴리스틱 함수값이 실제값보다 더 낮은 경우) 최단 경로를 찾는 것이 항상 좋은 방법이라고 할 수는 없다. 프로그램의 속도가 더 중요시되는 상황이라면 최단 경로를 포기하고 더 오래걸리는 경로를 찾도록 할 수밖에 없을 것이기 때문이다. (최단 경로만을 추구하는 것에 대해 회의적인 시각을 가진 글도 존재한다. 해당 글은 References의 [9]를 참고.)

아무튼, A* 알고리즘은 휴리스틱 함수가 admissible하기만 하다면 최단 경로를 보장한다(최적의 해를 찾아준다. 이를 optimal하다고 표현한다). (admissible하지 않으면 A* 알고리즘이 최단 경로를 항상 찾는다는 보장이 사라진다)

복잡도

A* 알고리즘의 시간 복잡도는 휴리스틱 함수에 의존한다. 최악의 경우에는 \(O(b^d)\)이다. 여기서 b는 branching factor(분기 계수)로, 각각의 노드에 연결되어 있는 엣지들의 평균 개수를 의미한다. d는 찾은 경로의 깊이를 뜻한다. 즉, source 노드부터 target 노드로 향하는 경로의 거리를 뜻한다. 경로 한 칸 한 칸 마다 평균 b개의 엣지들로 연결되어 있는 노드들을 거리 d까지 탐색해야하기에 나온 값이다.

공간복잡도도 마찬가지로 \(O(b^d)\)이다. 앞서 미로 찾기에서 인접한 노드들의 맨하탄 거리값들을 우선순위 큐에 저장해야 했다는 사실에서 알 수 있듯, 인접한 노드들의 각각의 evaluation function 값을 계산하고 이를 메모리 상에 저장해야 경로 탐색이 가능하기 때문이다.

Greedy best-first search

현재 노드까지 이동해온 거리를 고려하지 않고 오로지 휴리스틱 함수값에만 의존하는 해당 알고리즘의 또 다른 특징은, 이름에 greedy(탐욕적)가 붙어있듯, 오로지 눈 앞에 보이는 인접한 노드들 중 휴리스틱 함수값이 가장 낮은 (즉, target 노드까지의 거리가 가장 작게 측정되는) 노드로 향한다. 이는 현재 노드까지 오는데 걸린 거리(좀 더 포괄적으로는 “비용”이란 표현을 쓴다)를 고려하지 않으므로, 휴리스틱 함수값이 가장 낮은 인접한 노드로 향하는 것이 실제로 target 노드까지의 최단 경로로 이어지리란 보장은 없다.

즉, 해당 알고리즘은 항상 최적의 해를 찾지는 않는다. (not optimal)

다음은 이진 트리에서 숫자가 가장 큰 노드를 찾는 과정이다.

그림 5. 이진 트리 내에서 가장 큰 숫자 찾기. [3] 참조.

source 노드는 맨 위의 2라고 써진 노드이며, 해당 노드부터 시작하여 차례대로 아래로 내려가 가장 큰 숫자를 찾는다. greedy BFS 알고리즘을 사용하면 숫자 2 노드에서 인접한 노드인 4와 25중에서 가장 큰 숫자를 찾는다. (즉, 눈 앞에 있는 이득에만 집중한다) 그래서 해당 알고리즘은 오른쪽의 경로로 이동한다. 실제 가장 큰 숫자인 100은 정반대 방향에 존재하는 초록색 길에 있음에도 불구하고 말이다.

따라서 해당 알고리즘을 사용하여 최적의 답을 얻고자 한다면, 지역적인 범위에서의 최적성이 전역 범위에서의 최적성으로 귀결된다는 보장이 있는 문제에 한해서 적용해야 한다.

반대로 생각해보면, greedy BFS를 통해 그림 5의 문제를 풀 때, 실제 정답인 100에 도달하려면 총 3개의 엣지를 통과해야 하는 대신, greedy BFS는 25가 담긴 노드를 향해 1개의 엣지만 통과하면 된다. 즉, 해당 알고리즘은 정확성은 떨어지는 대신, 속도는 빠른 편이다.

greedy BFS의 시간, 공간 복잡도는 A* 알고리즘과 비슷하게 모두 \(O(b^m)\)이다. 그런데 주의해야할 점이, A* 알고리즘과 다르게 greedy BFS의 시공간 복잡도에 d대신 m이 써져 있다. d는 해의 깊이인 반면, m은 탐색 공간의 최대 깊이를 의미한다. 탐색 공간의 최대 깊이로 사용하는 이유는, A* 알고리즘은 휴리스틱 함수가 admissible하기만 하다면 최적성을 보장하나, greedy BFS는 항상 최적성이 보장되지 않기에 최단 경로가 아닌 깊이가 더 깊은 경로를 탐색할 수도 있기 때문이다. 따라서 greedy BFS의 시공간 복잡도가 A* 알고리즘보다 더 안 좋을 수도 있어 더 비효율적일 수도 있다.

알고리즘의 특성들

Termination

The property of termination(termination 특성)은 알고리즘이 언젠가는 탐색을 종료하는 지점에 도달할 것이라는 특성을 말한다. 즉, 결국에는 해를 찾거나, 아니면 더 이상 진행할 수 없는 종착점에 도달하게 된다는 뜻이다.

어떤 알고리즘의 완전성이나 최적성을 만족시킨다는 것은, 결국에 해를 찾는다는 것이고, 이는 언젠가는 알고리즘의 탐색이 종료된다는 것이다. 그래서 어떤 알고리즘이 완전성 또는 최적성을 가지면 그 알고리즘은 자동으로 “종료성”을 만족시킨다. 그 반대도 마찬가지이다. 어떤 알고리즘이 완전성 또는 최적성을 가지려면 해를 찾아야 하므로 알고리즘의 탐색이 언젠가는 멈춰야 한다. 따라서, 어떤 알고리즘이 완전성 또는 최적성을 가질려면 먼저 종료성을 가져야 한다.

해당 특성을 설명하는 곳이 Reference [3], [10] 밖에 없고, 영문 설명만 존재해서 한국어로 뭐라고 해석해야할지 모르겠음. 그래서 대략적으로 “종료성”이라고 해석하였다.

Completeness

completeness(완전성)은 만약 해가 존재한다면 알고리즘이 항상 그 해를 찾을 것이라는 특성을 의미한다. 만약 어떤 알고리즘이 완전성이 없다면, 그 알고리즘은 어떨 땐 해를 찾아도 또 어떨 땐 무한 루프에 빠지거나 정확하지 않은 해를 도출할 수 있다는 것이다.

Optimality

최적성은 어떤 알고리즘이 최적의 해를 도출하는 성질이다. 미로로 따지면 최단 경로를 도출해내는 것이다. 앞서 휴리스틱 함수와 평가 함수 설명 때 “비용”이라는 단어를 썼는데, 여기서도 해당 단어를 써보자면, 최적성은 “최소의 비용”으로 최적의 해를 내는 것이라고 볼 수 있겠다. 휴리스틱 함수의 값이 실제값과 정확히 똑같을 경우, 알고리즘은 항상 최적의 경로만을 추적하고, 더 이상의 불필요한 노드들을 탐색하지 않기에 탐색 시간도 덜 걸리고 그 만큼 메모리도 덜 쓰게 된다. 즉, 어떤 알고리즘의 최적의 해를 찾으면, 최소의 탐색 시간과 최소한의 메모리 사용을 보장하게 되는 것이다.

어떤 알고리즘이 최적성을 만족한다면, 이는 어찌되었건 해를 도출한다는 의미이므로, 완전성도 만족시킨다.

어떤 알고리즘이 admissible하다면, 그 알고리즘은 optimal하다.

어떤 알고리즘이 완전성을 보장받지 못하면, 최적성도 보장할 수 없다. 완전성이 없는 알고리즘은 때로 무한 루프에 빠지거나 부정확한 해를 도출할 수도 있다는 것인데, 이는 최적해를 보장하지 못한다는 말과 같기 때문이다.

그래프 알고리즘들의 특성

앞서 설명한 특성들을 토대로 앞서 다뤘던 그래프 알고리즘들을 다시 보자. DFS로 미로 탐색 시 최단 경로가 보장되지 않는다고 했다. 즉, DFS는 최적성을 보장하지 않는다. 그리고 유향 그래프일 경우, 해당 그래프에 cycle이 존재한다면 DFS는 해당 cycle에 빠질 수도 있어 무한 루프를 겪게 된다. 즉, 이 경우 종료성과 완전성이 보장되지 않는다.

BFS로 미로를 탐색할 때 항상 최단 경로를 찾는다. 즉, 최적성을 보장한다. 하지만 BFS 관련 페이지에서도 볼 수 있듯, 평균적으로 대부분의 노드들을 방문하기에 메모리 사용 용량이 타 알고리즘들에 비해 더 많을 것이다. BFS는 유향 그래프에 cycle이 있다고 하더라도 최단 경로가 존재하기만 한다면 cycle에 빠지지 않고 최단 경로로 탐색하기에 완전성도 보장한다고 볼 수 있다.

A* 알고리즘은 사용하는 휴리스틱 함수가 admissible 하기만 하다면 최적성을 보장한다. 또한, 그래프의 크기가 유한하고, 노드 간에 연결된 엣지를 통해 이동할 때 항상 비용의 값이 음수가 아니라면, 또는 branching factor가 유한하고 탐색할 때마다 비용이 고정되어 있다면(비용이 유한할 경우를 의미하는 것이 아닐까) 완전성을 보장한다.

greedy BFS는 일반적으로 최적성과 완전성을 보장하지 않는다고 한다.

Reference

[1] George T. Heineman, “Learning Algorithms: A Programmer’s Guide to Writing Better Code”, (O’Reilly, 2021)

[2] What is the A* algorithm?

[3] What Is a Heuristic Function? | Baeldung on Computer Science

[4] Heuristics

[5] A* Pathfinding Algorithm | Baeldung on Computer Science

[6] AI | Search Algorithms | Greedy Best-First Search | Codecademy

[7] Greedy Best first search algorithm - GeeksforGeeks

[8] Informed Search Algorithms in AI - Javatpoint

[9] 최단 경로를 찾는게 항상 옳은가에 대한 글. Don’t follow the shortest path!

[10] chat-gpt